Sidebar
keynote:2013-lesson01
Table of Contents
第一讲 引言与点估计方法
0. 引言
提要
- 问题的背景
- 数据驱动的基本概念
- 数据驱动的应用与意义
当今计算机科学最大的现状和挑战
- 大量企业正在收集数据:
- Google, Apple, Facebook, IBM, Microsoft, Amazon, …
- 中国: 3Q War, Taobao, Sina, Baidu
- 数据,数据,数据……
- 需要大量乏味的重复的工作才能创建数字化的世界
- 需要寻找新的交互方式,创造新类型的媒体
- 花费高的代价才能请专家(科学家、工程师、电影制作人员、图形设计师、优秀艺术家和游戏设计人员)来完成工作
- 需要高效地处理已经存在的数据,并通过它们获得新的数据
计算机是高效运行的机器
- 各种图像、场景,只要人能够创造,就可以利用计算机来得到它
- 但是如何来创造这些图像、场景
完全过程化合成VS完全数据化
- 为电影中的一个角色创造动作
- 完全过程化合成
- 动作比较连贯,但是很容易让人觉得是伪造的,很少在实际中这样用
- 完全手工制作或者完全数据化
- 效果质量很高,但是连贯性不好
- 把两者结合起来的混合方法或许是最好的!?
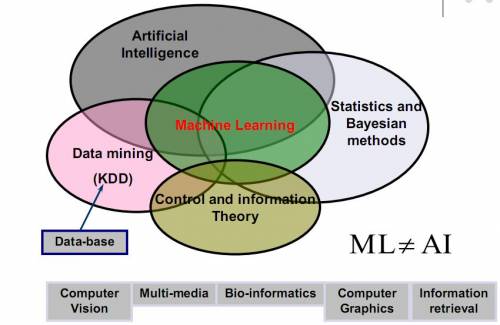
贝叶斯推理
- 关于不确定性的一个规则模型
- 非结构化数据的通用模型
- 数据拟合和不确定分析的有效算法
但是,当前它通常被当做一个黑盒来使用
确定性 VS 机率性
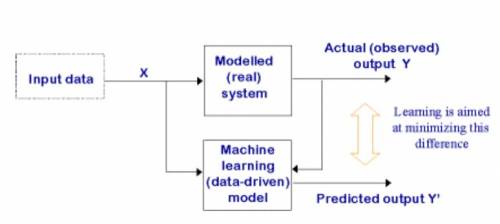
数据驱动模型
数据驱动相关技术
- 学习系统不只是用来解决一个问题,而是基于一些特征来使系统本身更加优化:
- 关于系统应该如何做出响应的一些例子
- 关于系统在解决问题的过程中反复试验学习到的经验
- 不同于通常的计算机科学,去实现一个未知的功能;仅仅是处理已知的输入输出数据对(学习过程中的训练例子)
学习问题的主要分类
- 学习情景根据训练例子中提供的有效信息的改变而改变
- 监督的:需要正确的输出
- 分类:输入N个目标,输出结果为选择其中一个(语音识别、目标辨认、医学诊断)
- 回归:输出准确值(预测未来的市场价格、温度)
- 部分监督的:只输出一部分有效结果
- 无监督的:没有反馈,需要对输出进行自我评估
- 聚类:聚类是指将数据分割成连贯的群集的技术
- 结构异常识别:检测超出正常范围的数据点
- 加强的:标量反馈,可能暂时推迟
更多
- 时间序列分析
- 降维
- 模型选择
- 泛型方法
- 图形建模
为什么学习数据驱动有用?
- 开发强化的计算机系统
- 能够自动适应用户,更加符合用户要求
- 旧的系统往往很难获得必要的知识
- 发掘大型数据库中离线的新数据挖掘模式
- 提高对人的认识,生物学习
- 提供具体的理论计算分析,预测
- 分析大脑的学习过程中的爆发式活动
- 研究时机很好
- 数据量的快速增长
- 计算机不再昂贵而且功能强大
- 理论得到了很好的发展,有一系列的算法组件
对计算机科学和技术有用吗?
- 赞成方:所有事物都是机器学习,所有事物都是人的调整
- 在有些时候,这个说法是正确的
- 反对方:虽然是对“学习”的一种深化,但还有其它更强大和有效的算法。
- 问题分类
- 通用模型
- 通过概率进行推算
- 相信数学的魔力
怎样才是一个成功的学习算法?
- 计算效率
- 鲁棒性
- 统计稳定性
一些实际应用
- Google!
- 目标识别和辨认——学习的力量
- 文档处理——贝叶斯分类器
- 网格处理——数据聚类和分割
- 纹理合成和分析——隐式马尔科夫模型
- 反射纹理合成——降维
- 人体建模——降维
- 图像处理和合成——图形建模
- 人体运动合成——时间序列分析
- 视频纹理——强化学习
总结
- 学习系统就是这样看上去很难但非常有用的东西

- 关键字:
- 名词:数据、模型、模式、特征
- 形容词:概率性的、统计的
- 动词:拟合、推理、挖掘
作业
- 在你的研究方向上寻找学习系统的潜在应用
参考文献
- Reinforcement learning: A survey
1. 点估计
最大似然, 最大化后验估计, 贝叶斯估计, 回归方法与过拟合问题
你将要学习
- 点估计
- 最大似然估计(MLE, Maximal Likelihood Estimation)
- 贝叶斯学习(Bayesian Learning)
- 最大化后验(MAP, Maximize A Posterior)
- 高斯估计
- 回归(Regression)
- 基础方程 = 特性
- 方差和的最优化
- 回归与高斯估计的关系
- 倾向与方差的折中
你的第一个咨询工作
一个北京的IT亿万富翁咨询你如下问题: * 富:我有一些图钉,我将其抛出,那么它尾部朝上的概率是多少? * 你:那么扔几次看看吧... * (图待上传) * 你:概率是3/5 * 富:这是为什么呢? * 你:这是因为...
二值分布
- 设头朝下的概率 P(Heads)= θ,尾朝下的概率 P(Tails)=1-θ,发生的事件D={T,H,H,T,T}
- 抛图钉是一种独立重复分布(i.i.d. Independent Identically distributed)
- 每一次实验彼此独立
- 根据二值分布的分布概率相同
- 如果一个事件D包含αH个头朝下的概率和αT个尾朝下的概率,这样事件的概率是:
P(D|θ)=θαH(1-θ)αT
最大似然估计
- 数据:观察事件集合D包含α H 个头朝下的事件和α T 个尾朝下的事件
- 前提:二值分布
- 在优化问题中对θ进行学习:
- 目标函数是什么?
D = {T, H, H, T, T} - MLE: 找出使观察到的现象的概率最大化的 θ
\begin{aligned}
\hat{\theta} & = \arg\max_\theta P(D|\theta) \\
& = \arg\max_\theta \ln P(D|\theta) \\
& = \arg\max_\theta \ln (\theta^{\alpha_H} (1-\theta)^{\alpha_T}) \\
& = \arg\max_\theta \alpha_H\ln\theta + \alpha_T\ln(1-\theta) \end{aligned}
& = \arg\max_\theta \ln P(D|\theta) \\
& = \arg\max_\theta \ln (\theta^{\alpha_H} (1-\theta)^{\alpha_T}) \\
& = \arg\max_\theta \alpha_H\ln\theta + \alpha_T\ln(1-\theta) \end{aligned}
- 导数为0时取极值,则有
\hat{\theta} = \frac{\alpha_T}{\alpha_H+\alpha_T} = \frac{3}{2+3}
我需要抛多少次?
θ^ = αT / (αH + αT)
对话片段 * 富:我抛了两个头朝上和三个尾朝上 * 你:θ是3/5,我可以证明 * 富:如果我抛了20个头朝上和30个尾朝上呢 * 你:答案依然一样,我可以证明 * 富:能多解释一下吗 * 你:越多约好吗 * 富:所以我才会给你这么多报酬啊
简单边界(基于Höffding不等式)
- 对于N = αH + αT 和 θ^ = αT / αH + αT,有
- 令θ*为真实值,对任意ε>0,有
P(|θ^ - θ*|≥ε)≤2e-2Nε^2
COPYRIGHT, 2013
keynote/2013-lesson01.txt · Last modified: 2023/08/19 21:02 (external edit)
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 4.0 International