Sidebar
Table of Contents
第九课
9.1 偏微分方程:简介
9.1.1 偏微分方程的历史
9.1.2 偏微分方程初步 9.1.2.1 曲线积分:弧长、参数、坐标 9.1.2.2 曲面积分:面积、坐标 9.1.2.3 微分方程基本概念
9.1.3 三个基本的偏微分方程
9.1.4 偏微分方程的求解
9.1.1 偏微分方程的历史
历史:十七世纪以前
17世纪以前,中国在科技上占有绝对的领先地位。中国古代的科技思想主要是《易经》所宣扬的以物相数的思想。
随着牛顿发明了微积分,西方的生产科技力量迅速增长。
微分方程几乎是和微积分同时产生的,这使得人们对于自然界有了更加本质的认识。 微分方程或微积分是人们认识自然界的有效工具,但不是唯一的工具。
历史:十七世纪
17世纪,随着 Newton, Lebiniz 等发明了微积分,数学家们开始用微分变化的思想来解释各种物理现象。
不久,这些微分符号出现在一些方程里,最原始的微分方程就这样产生了。
但是人们发现这些微分方程并不好求解,一般只有在它们的积分变量可分时才可解。
历史:十八世纪
18世纪早期,随着人们将微分方程应用到星体运动等物理现象的研究,对微分方程有了进一步的研究。
Jacob Bernoulli 仔细研究了用微分方程解决星体运动的问题。
Taylor 用级数的方法来求解微分方程,并提出了有限差分的方法。
这段时期人们虽然对微分方程的研究有了很大进步,但是还没有形成一个一般的理论。
早期人们研究微分方程的主要障碍就是如何求解方程,有些方程看似简单,但实际上极为复杂。
Euler 根据他对函数的结构和性质的了解,发现了函数是理解和解决微分方程的关键。他发明了一个一般的解决不同类方程的步骤。同时他还建立了一些微分方程模型来解决一些应用的问题。
在Euler之后许多数学家扩展或改进了他的思想。
Lagrange 可能是第一位有足够的理论和工具来分析微分方程的数学家。1788年他提出了动态系统的一般运动方程,即 Lagrange 方程. Laplace 的对太阳系稳定性的研究导致了微分方程的更大的进展,包括更好的数值技术和对积分更深入的理解。1799年他提出了Laplacian 方程。 Fourier 在求解热扩散方程上做出了很大的贡献,Fourier级数分析的方法是学习震动现象的重要工具。
历史:十九世纪
19世纪初期,随着Gauss和Cauchy对复变函数的研究的贡献,人们对微分方程的认识也有了很大的进展。
Gauss 建立了势理论,并发现复变量是理解许多应用中的微分方程的关键。
Cauchy 将微分方程应用到对流体表面波传导的建模中。他是第一个开始对微积分和微分方程进行严格分析的人,也是第一个对复数建立系统理论并用 Fourier变换的方法求解微分方程的人。
Poisson 将他对微分方程的理解应用到弹性和震动理论的研究。他的大部分工作都是分析和求解微分方程。
George Green 同样将已有的微分方程应用到电磁场理论中。在1828年他发表了《 An Essay on the Application of Mathematical Analysis to Electricity and Magnetism 》。他的理论是像Thomson, Stokes, Rayleigh, Maxwell等人工作的基石。
在19世纪中叶,为了解决微分方程组问题,一些新的理论产生出来。
Jacobi 发展了行列式和变换的理论来解决微分方程问题。
Cayley 在行列式理论的基础上提出了矩阵运算理论。他是矩阵论的奠基者。
Josiah Gibbs 对热动力系统,电磁场理论和机械理论都有贡献。因为他在微分方程系统方面的工作,他被誉为‘向量分析之父’。
在19世纪末,对偏微分方程的主要工作都是在理论分析方面。
Lipschitz 建立了一阶微分方程的存在性定理。
Hermite 在函数理论和方程求解方面也有很重要的贡献。其中Hermite方程后来被证明在求解Schrodinger的波动方程很有用。
Bernhard Riemann 在微分方程的理论基础的建立上有很大的贡献。他的结果在动力学和物理中的许多方面都很有用。
查尔斯.巴贝奇(1791 -1871 ),鉴于当时构造数表很麻烦,发明了差分机(又称差分引擎(未完成))。
分析机(设计稿), 基于机械运算,具有与现代计算机类似的体系结构。 差分机2号,由英国伦敦科学博物馆与1985-2002年间实现。
历史:数值求解
微分方程另一个主要的推动力是有效的数值算法。
Carl Runge 在微分方程数值解方面做了许多工作。
他的研究中用了很多数学以至于物理学家们认为他是数学家,而他的工作都是为了解决物理问题以至于数学家们都认为他是物理学家。 著名的 Runge-Kutta方法现在依然在被使用。
到了20世纪后半叶,由于计算机技术的发展,许多数学家和计算机学家在用微分方程数值解方面做了许多工作。
小结
微分方程涉及物理等学科的各个方面。它的进步是和生产实践分不开的。
微分方程的发展是和微积分的发展密切相关的。
近代的计算机技术使得微分方程数值解成为可能。
微积分初步之曲线积分
— 叶敏超
- 对弧长的曲线积分(第一类曲线积分)
定义:
设L为xOy平面内一条光滑曲线弧,函数f(x,y)在L上有界。用L上的点M_1,M_2,\ldots,M_{n-1}把L分成n小段。 设第i个小段的长度为\Delta {s_i},又({\xi _i},{\eta _i})为第i小段上任意取定的一点。 做乘积f({\xi _i},{\eta _i})\Delta {s_i},并做和\sum\limits_{i = 1}^n {f({\xi _i},{\eta _i})\Delta {s_i}} ,如果当各小弧段长度的最大值\lambda \to 0时,和的极限存在,则称此极限为f(x,y)在曲线L上对弧长的曲线积分或第一类曲线积分。
存在条件:
f(x,y)在光滑曲线弧L上连续。
推广:
f(x,y,z)在空间曲线\Gamma上的对弧长的曲线积分为
注意:
1.若L分段光滑(L=L_1+L_2),
2.若L为闭曲线,则f(x,y)在L上对弧长的曲线积分可记为:
性质
(1) \int_L {[f(x,y) \pm g(x,y)]ds} = \int_L {f(x,y)ds} \pm \int_L {g(x,y)ds}
(2) \int_L {kf(x,y)ds} = k\int_L {f(x,y)ds} (k为常数)
(3) \int_L {f(x,y)ds} = \int_{L_1} {f(x,y)ds} + \int_{L_2} {f(x,y)ds} (L=L_1+L_2)
- 对弧长曲线积分的计算
设f(x,y)在曲线L上有定义且连续,L的参数方程为\begin{cases} x = \phi (t) \\
y = \psi (t)\end{cases},(\alpha \le t \le \beta ),其中\phi(t)、\psi(t)在[\alpha,\beta]上具有一阶连续导数,则
注意:
1.积分下限\alpha要小于积分上限\beta。
2.f(x,y)中x,y不彼此独立, 而是相互有关的。
特殊情形
(1)L:y = \psi (x)\quad \quad a \le x \le b
(2)L:x = \phi (y)\quad \quad c \le y \le d
(3)L:r = r(\theta ),\quad \quad \alpha \le \theta \le \beta
- 几何与物理意义
(1)当f(x,y)表示L的线密度时,
(2)当f(x,y) \equiv 1时,
(3)当f(x,y)表示立于L上的柱面在点(x,y)处的高时,
(4)曲线弧对x轴及y轴的转动惯量:
(5)曲线弧的重心:
- 对坐标的曲线积分
定义
设L为面xoy内从点A到点B的一条有向光滑曲线弧,P(x,y),Q(x,y)在L上有界。在L上沿L的方向任意插入一点列{M_1}({x_1},{y_1}),\;{M_2}({x_2},{y_2}), \cdots ,{M_{n - 1}}({x_{n - 1}},{y_{n - 1}})把L分成n个有向小弧段\widehat{M_{i-1}M_i}(i = 1,2, \cdots ,n;{M_0} = A,\;{M_n} = B)。设\Delta {x_i} = {x_i} - {x_{i - 1}},\;\;\Delta {y_i} = {y_i} - {y_{i - 1}},点({\xi _i},{\eta _i})为M_{i-1}M_i上任意取定的点。如果当各小弧段长度的最大值\lambda \to 0时,\sum\limits_{i = 1}^n {P({\xi _i},{\eta _i})\Delta {x_i}} 的极限存在,则称此极限为函数P(x,y)在有向曲线弧L上对坐标x的曲线积分(或称第二类曲线积分)记作
存在条件:当P( x, y), Q( x, y)在光滑曲线弧L上连续时第二类曲线积分存在。
组合形式:
推广:
空间有向曲线弧\Gamma
性质
(1)如果把L分成L_1和L_2(L=L_1+L_2),则
(2)设L是有向曲线弧,-L是与L方向相反的有向曲线弧,则
对坐标的曲线积分的计算
曲线L:\begin{cases} x=\phi(t)\\y=\psi(t)\end{cases} ,起点t=\alpha,终点t=\beta。dx = \phi'(t)dt,dy = \psi'(t)dt
注意:
1.定积分的下限\alpha不一定要小于上限\beta;
2.f ( x, y)中x, y不彼此独立,而是相互有关的。
特殊情形
(1)L:y=\psi(x),x起点为a,终点为b。则L: \begin{cases}x=x \\
y=\psi(x) \end{cases},dx=dx,dy=\psi'(x)dx。
(2)L:x=\phi(y),y起点为c,终点为d。则L: \begin{cases}x=\phi(y) \\
y=y \end{cases},dx=\phi'(y)dy,dy=dy。
推广
\Gamma:\begin{cases}x=\phi(t)\\y=\psi(t)\\z=\omega(t)\end{cases},t起点\alpha,终点\beta。
= \int_\alpha ^\beta {\{ P[\phi (t),\psi (t),\omega (t)]\phi '(t)} + Q[\phi (t),\psi (t),\omega (t)]\psi '(t) + R[\phi (t),\psi (t),\omega (t)]\omega '(t)\} dt
两类曲线积分之间的联系
设有向平面曲线弧为L:\begin{cases}x=\phi(y)\\\\y=\psi(t)\end{cases},其切向量为\overrightarrow T = \{ \phi '(t),{\rm{ }}\psi '(t)\} 。L上点(x,y)处的切向量的方向角为\alpha,\beta,
则有
两类曲线积分之间的区别
对弧长的曲线积分没有方向,对坐标的曲面积分有方向。
格林公式
设闭区域D由分段光滑的曲线L围成,函数P(x, y)及Q(x, y)在D上具有一阶连续偏导数,则有
格林公式表明了沿闭曲线的曲线积分与其所围区域的二重积分之间的联系。
9.1.2.3 微分方程基本概念
— 王耀光 2011/06/15 14:22
常微分方程和偏微分方程
(1)常微分方程(函数为单变量)
定义
2阶偏微分方程的定义:
例如:
分类
(1)一阶,二阶,…:偏导的最大次数;
(2)线性,非线性,拟线性(方程对最高项是线性的);
(3)齐次,非齐次:是否每个变量的阶数都相等;
一阶拟线性方程组:
定解条件
边界条件(BVP)和初始条件(IVP):
偏微分方程一般可能有无穷多个解。实际中只要求解在某一定义域范围之内的解即可,
如果在边界上限定了边界条件和初始条件,那方程的解一般是唯一的。这样才有物理意义。
边界条件:
(1)Dirichlet 条件:给出u在∂S上的值;
(2)Neumann 条件:给出∂S/∂n在∂S上的值;
(3)Robin 条件:给出au + b*∂u/∂n在∂S上的值(包括前两种);
定解问题的适定性
稳定性:当初始数据或边界数据有微小变化时解的变化也应当微小。 适定性:如果定解问题的解在该函数空间存在,唯一并且稳定。 对两个变量的二阶拟线性方程:
如果对于固定的(x,y,u), 有:
二次线性偏微分方程的分类
叠加原理
在物理,力学和化学等学科中,许多自然现象具有叠加效应,即几种不同因素同时出现时所产生的效果等于各个因素分别单独出现时产生的叠加(即总和)。 用数学的话讲,对所有线性系统 F(x)=y,其中 x 是某种程度上的刺激(输入)而 y 是某种反应(输出),刺激的叠加(即“和”)得出分别反应的叠加: F(x1+x2+...)=F(x1)+F(x2)+... 在数学中,这个性质更常被叫做可加性。在绝大多数实际情形中,F 的可加性表明它是一个线性映射,也叫做一个线性函数或线性算子。
变分原理
最小位能原理(Hamilton原理):任何力学系统,若给定t=t0的起始状态 和时刻t=t1的终结状态,则真实运动区别于任何容许运动的地方在于:真实运动 使定积分(T为总动能,U为总势能)。
关于一阶变分的定义说明:
假设真实运动函数为:u(x,y,z,t)
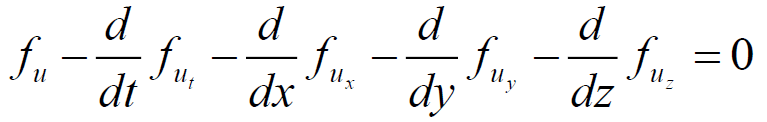
9.1.3三个基本的偏微分方程
— 伊灯 2011/06/15 16:00
双曲线方程(波动方程)
— 伊灯 2011/06/15 16:00
双曲线方程
定义
波动方程
波动方程或称波方程(wave equation)是一种重要的偏微分方程,主要描述自然界中的各种的波动现象,包括横波和纵波,例如声波、光波和水波。波动方程抽象自声学,电磁学,和流体力学等领域。
历史上许多科学家,如达朗贝尔、欧拉、丹尼尔•伯努利和拉格朗日等在研究乐器等物体中的弦振动问题时,都对波动方程理论作出过重要贡献。 波动方程是双曲形偏微分方程的最典型代表,其最简形式可表示为:关于位置x 和时间t 的标量函数u(代表各点偏离平衡位置的距离)满足:
'c'通常是一个固定常数,代表波的传播速率。在常压、20°C的空气中c为343米/秒。在弦振动问题中,c 依不同弦的密度大小和轴向张力不同可能相差非常大。而在半环螺旋弹簧(一种玩具,英文商标为 Slinky)上,波速可以慢到1米/秒。
在针对实际问题的波动方程中,一般都将波速表示成可随波的频率变化的量,这种处理对应真实物理世界中的色散现象。此时,c 应该用波的相速度代替:
'非线性波动方程':
u的表达式将包含一个马赫因子(对沿流动方向传播的波为正,对反射波为负)。
抛物线方程(热传导方程)
抛物型偏微分方程是一类二阶偏微分方程, 描述自然科学中广泛的问题, 包括热能的扩散以及布莱克-斯科尔斯模型. 这些问题, 通常被称为演化问题.
数学上, 具有以下形式的偏微分方程
一个简单的抛物型偏微分方程是一维的热传导方程:
热传导方程的主要推广具有形式
椭圆方程(位势方程)
泊松方程(Poisson's equation)是数学中一个常见于静电学、机械工程和理论物理的偏微分方程式,因法国数学家、几何学家及物理学家泊松而得名。 泊松方程式为
在三维坐标系,可以写成:
如果沒有f(x,y,z),这个方程式就会变成一个齐次方程,这个方程称作“拉普拉斯方程”:
泊松方程可以用格林函数來求解;如何利用格林函数來解泊松方程可以参考screened Poisson equation。现在有很多个数值解。像是relaxation method,不断回圈的代数法,就是一个例子。 — 伊灯 2011/06/15 20:25
格林公式
— 李润泽 2011/06/16 14:01
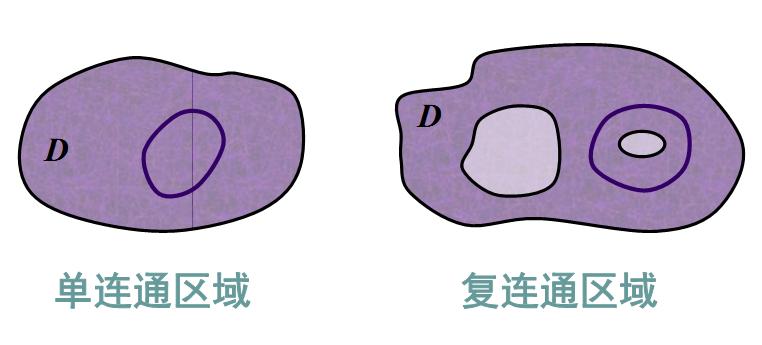
设D为平面区域,如果D内任一闭曲线所围成的部分都属于D,则称D为平面单连通区域,否则称为复连通区域.
定理1
设闭区域D由分段光滑的曲线L围成,函数P(x,y)及Q(x,y)在D上具有一阶连续偏导数,则有
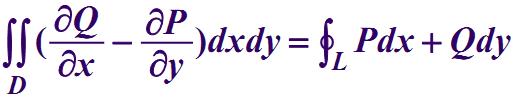
其中L是D的取正向的边界曲线,
面积曲面积分
定义
设Σ为光滑的有向曲面,函数在Σ上有界,把Σ分成n块小曲面\DeltaSi(\DeltaSi同时又表示第i块小曲
面的面积),\DeltaSi在xoy面上的投影为(\DeltaSi)xy,(\xii,\etai,\zetai)是\DeltaSi上任意取定的一点,如果当各小块曲面的直径的最大值\lambda→0时,
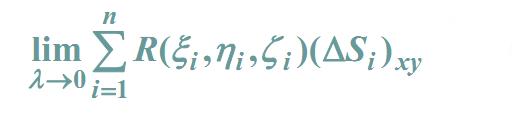
存在,则称此极限为函数R(x,y,z)在有向曲面Σ上对坐标x,y的曲面积分(也称第二类曲面积分)
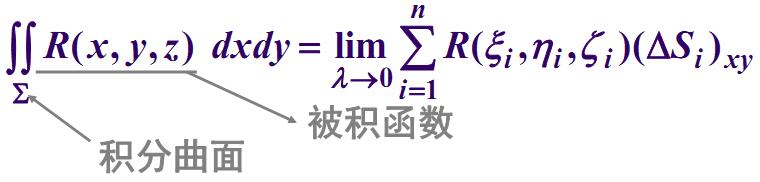
Gauss公式
设空间闭区域\Omega由分片光滑的闭曲面Σ围成。函数P(x,y,z),Q(x,y,z),R(x,y,z)
在\Omega上具有一阶连续偏导数,则有公式
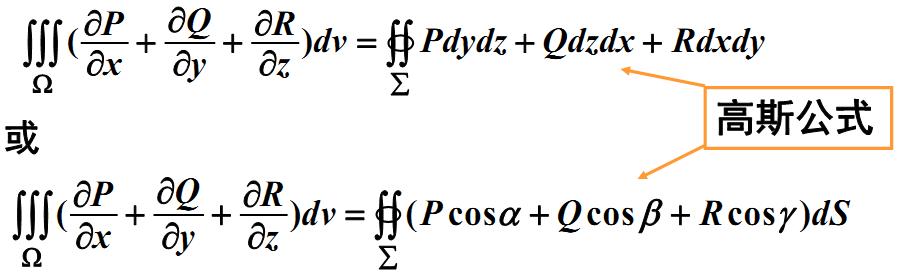
这里\Sigma是\Omega的整个边界曲面的外侧,\cos\alpha,\cos\beta,\cos\gamma
是\Sigma上点(x,y,z)处的法向量的方向余弦.
Gauss公式的实质 表达了空间闭区域上的三重体积分与其边界曲面上的曲面积分之间的关系.

