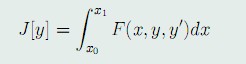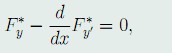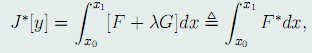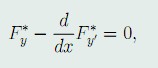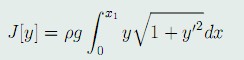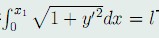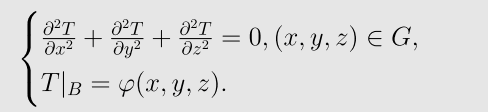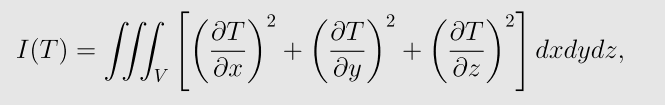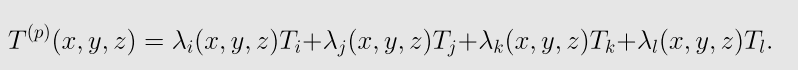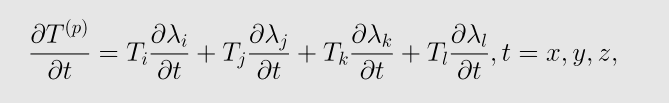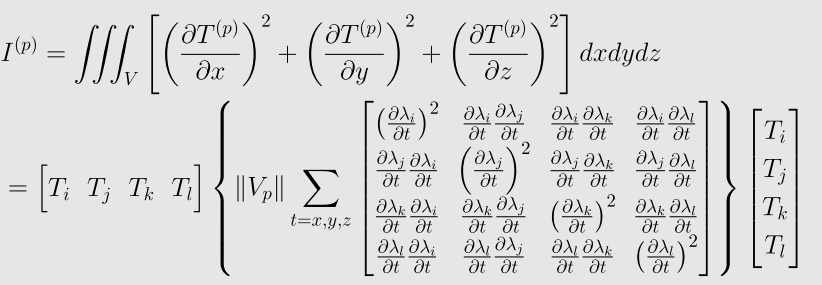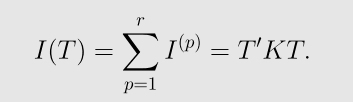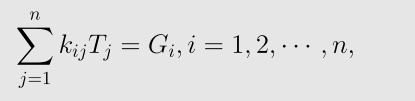Sidebar
Table of Contents
第八课
4 条件极值的变分问题
4.1 附有约束条件φ=0的变分问题
问题的提出:这一节,我们主要研究泛函
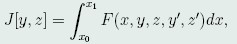 (40)
(40)
满足边界条件
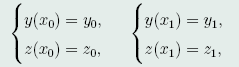 (41)
(41)
约束条件φ(x,y,z)=0,(42)
的极值问题,导出泛函J的极值曲线应满足的条件。
几何意义:这两位问题的几何意义是:在曲线φ(x,y,z)=0上求一条曲线
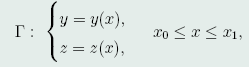
使得泛函(40)在Γ上取得极值。类似于有条件函数极值的Larange方法,有条件泛函极值问题也可以化为无条件极值来处理。
Lagrange定理
设y(x),z(x)是泛函(40)在边界条件(41)和约束条件(42)下的极值函数。如果在曲线
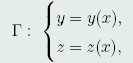
上,φ_y,φ_z至少有一个不为零,则必存在函数λ(x),是y(x),z(x)满足泛函
 (43)
(43)
的Euler方程组
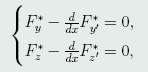 (44)
(44)
其中,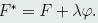 。
。
证明:不妨设在曲线Γ上,φ_z≠0,按隐函数存在定理,可由(42)式确定一个函数z=ψ(x,y),将它代入(40)式,得
 (45)
(45)
其中,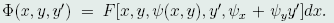 这样,就把泛函(40)的条件极值问题转化成了泛函(45)的无条件极值问题。
泛函(45)的Euler方程为:
这样,就把泛函(40)的条件极值问题转化成了泛函(45)的无条件极值问题。
泛函(45)的Euler方程为:
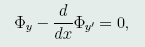 (46)
(46)
计算 得:
得:
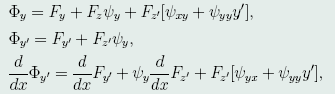
代入(46)式,得:
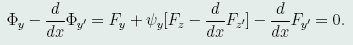
注意到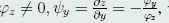 ,于是有
,于是有
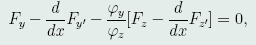
或
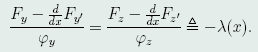
因此,存在函数λ(x),使极值函数y(x),z(x)满足方程组
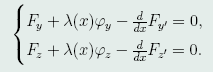
令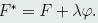 ,则
,则 ,于是,上式变成
,于是,上式变成
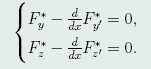
这方程组就是以F*为被积函数的泛函的Euler方程组。
例1:在空间曲面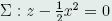 上求连接两点O(0,0,0)和B(1,1/2,1/2)的最短曲线。
上求连接两点O(0,0,0)和B(1,1/2,1/2)的最短曲线。
解:问题归结为在曲面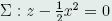 上求一曲线
上求一曲线
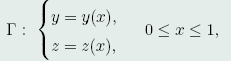
使其满足边界条件

且使泛函
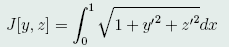
取极小值。
按照Lagrange定理,做辅助泛函

其中,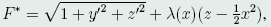 ,由Euler方程组(44)式及约束条件,有
,由Euler方程组(44)式及约束条件,有

由上面第一式得,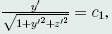 ,将上面第三式代入此式,得
,将上面第三式代入此式,得
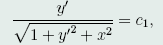
或

积分后,可得
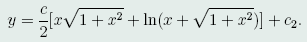
因为所求曲线过点O(0,0,0)和B(1,1/2,1/2),因此可确定出
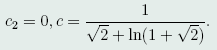 (47)
(47)
于是,所求曲线为
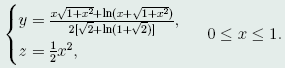
连接点O与B的弧段的长度为
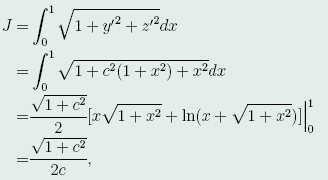
其中的常数c如(47)所示。
例2:试求出圆柱面x^2+y^2=R^2上,连接点P_1(x_1,y_1,z_1)与点P_2(x_2,y_2,z_2)的最短曲线。
解:设圆柱面的参数方程为
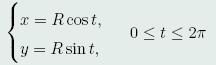
因为点P_1,P_2在圆柱面上,故所求曲线P_1P_2的x,y坐标与圆柱面的相同,只要求出z坐标z=z(t)即可。
设P_1,P_2点对应的参数为t_1<t_2,则P_1P_2的弧长为
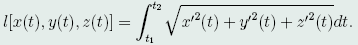
于是,问题化为:求过P_1,P_2且位于圆柱面上的曲线,使泛函l取极小值。
做辅助泛函
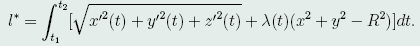
将x=Rcost,y=Rsint代入上式,得

其中,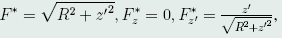 l*的Euler方程为
l*的Euler方程为
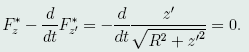
初积分为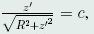 则,
则, 再积分,有z=c_1t+c_2.故所求最短曲线是圆柱螺线
再积分,有z=c_1t+c_2.故所求最短曲线是圆柱螺线
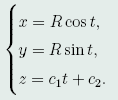
其中,c_1,c_2由P_1(x_1,y_1,z_1),P_2(x_2,y_2,z_2)确定。
4.2 等周问题
问题的提出:以前研究的等周问题是狭义的等周问题,一般的等周问题是指在泛函约束(等周条件):
K [ y ] = \int_{x_0}^{x_1} {G(x,y,y') dx} = l (48)
及边界条件:
y(x_0) = y_0, y(x_1) = y_1 (49)
中求泛函:
的极值函数,其中 G , l, y等均是给定的函数或常数
Euler定理
上述广义的等周问题可以由下述Euler定理解决,它把条件极值的变分问题化成了无条件极值的变分问题。
Euler定理: 若曲线\Gamma : y = y(x) 在等周条件(48)及边界条件(49)下,使泛函(50)达到极值,则存在常数\lambda,使y(x)满足泛函:
的Euler方程:
其中, F^* = F + \lambda G .
证明过程利用到在上一节中由方程约束的极值问题已经得到解决,把泛函约束变成方程约束的条件来处理。
求解等周问题的方法:根据Euler定理,得到了求泛函(50)在等周条件(48)和边界条件(49)下的极值函数的解题方法:
作辅助泛函:
其中,\lambda为待定常数,然后,由J^*的Euler方程
与等周条件及边界条件联立求解。
等周问题相关实例
例1:在XOY平面上求通过两定点A, B, 其坐标值分别为(x_0, y_0)和(x_0, y_0), 且长度为定值l的曲线y = y(x), 使得所围城的曲边梯形的面积最小。
例2:求悬链形状问题的解,即求泛函
在边界条件y(x_0) = y_0, y(x_1) = y_1 和约束条件
下的极值曲线
例3: 在平面上长度为定值l的所有闭曲线中,求一曲线C,使它所围成的面积最大
5 变分问题中的直接法
前面所讨论的变分问题,都可归结为Euler方程或奥氏方程的求解问题。但是在大多数情况下要求得变分问题的精确解是很困难的, 有时甚至是不可能的。因此有必要用其他方法求变分问题的解。这就是所谓的直接法。
5.1 里兹法(Ritz)
基本思想:用某个函数序列的线性组合逼近泛函极值问题的极值曲线。
问题:设泛函为: J[y] = \int_{x_0}^{x_1}F(x,y,y')dx (54)
边界条件为:y(x_0)=0, y(x_1)=0 (55)称为齐次边界条件。如果边界条件不是齐次的,如y(x_0)=y_0, y(x_1)=y_1,则可令: y(x)=z(x)+{x-x_1\over x_0-x_1}y_0+{x-x_0\over x_1-x_0}y_1 (56)
有z(x_0)=0, z(x_1)=0,问题(54),(55)化为齐次边界的变分问题,J[y]=J_1[z]=\int_{x_0}^{x_1}F_1(x,z,z')dx, z(x_0)=0,z(x_1)=0
基本步骤:设泛函J[y]的极值曲线在曲线簇Y内,Y构成线性空间,用里兹法求泛函J[y]近似解的步骤如下:
- 选取Y的基函数:φ_1(x),φ_2(x),\cdots,φ_n(x),\cdots(57),对任意y(x)∈Y,y(x)都可以表示为{φ_i(x)}的有限维或无限维线性组合。特别地,对极值函数f(x),也有,f(x)=c_1φ_1(x)+c_2φ_2(x)+\cdots+c_nφ_n(x)+\cdots
- 对每个n,考虑由φ_1,φ_2,\cdots,φ_n生成的线性子空间Y_n,设y_n(x)=\sum^n_{i=1}a_iφ_i(x)∈Y_n,由泛函J[y]就确定了n元函数:J[a_1,\cdots,a_n]=J[y_n]=\int_{x_0}^{x_1}F[x,\sum^n_{i=1}a_iφ_i(x),\sum^n_{i=1}a_iφ'_i(x)]dx.
- 对每个n,选取a^n_1,a^n_2,\cdots,a^n_n,使J[y_n]取极值。也就是方程组{\partial \over \partial a_i}J[y_n]=0, i=1,2,\cdots,n,来确定a^n_1,a^n_2,\cdots,a^n_n,然后用得到的函数f_n=\sum^n_{i=0}a^n_iφ_i(x)作为变分问题的近似解。
几点说明:
- 上面求得的f_n是序列(57)中前n个函数所有可能的线性组合中使泛函J[y_n]达到极值的函数。这样得到的序列f_1,f_2,\cdots,f_n,\cdots成为J[y]的极小化序列。
- 因为,Y_1⊂Y_2⊂\cdots⊂Y_n\cdots,所以,J[f_1]≥J[f_2]≥\cdots≥J[f_n]\cdots,并且,\lim_{n \rightarrow ∞}J[f_n]=J[f]。
- 但是,并不能保证\lim_{n \rightarrow ∞}f_n;即使存在,也不一定收敛于J[y]的极限函数f。但对常用函数来说,f_n不仅逐点收敛,而且一致收敛于f。因此,如果只限于讨论前n项和f_n=\sum^n_{i=0}a^n_iφ_i(x),那么,f_n就是变分问题的近似解。
- φ_n(x)=(x-x_0)^n(x_1-x),n=1,2,\cdots
- φ_n(x)=(x_1-x)^n(x-x_0),n=1,2,\cdots
- φ_n(x)=sin{nπ(x-x_0)\over x_1-x_0},n=1,2,\cdots
例子:用Ritz法求解变分问题J[y]=\int_{0}^{1}(y'^2 - y^2 - 2xy)dx,y(0)=y(1)=0,近似解。
解:取 φ_n(x)=x^n(1-x),n=1,2,\cdots,显然, φ_n(0)=φ_n(1)=0.
- 求一级近似解.
作y_1=c_1φ_1(x)=c_1x(1-x), 则y'=c_1(1-2x), 代入泛函,得:J[y_1]=J[c_1]=\int_{0}^{1}[c_1^2(1-2x)^2 - c_1^2x^2(1-x)^2-2c_1x^2(1-x)]dx = {3 \over 10}c_1^2-{1 \over 6}c_1。选取c_1, 使J[c_1]取极值。为此,令{dJ \over dc_1}={6 \over 10}c_1-{1 \over 6}=0, 得c_1={5 \over 18}. 故,一级近似解为f_1={5 \over 18}x(1-x).
- 求二级近似解.
作y_2=c_1φ_1(x)+c_2φ_2(x)=c_1x(1-x)+c_2x^2(1-x)=x(1-x)(c_1+c_2x),则y'_2=(1-2x)(c_1+c_2x)+c_2x(1-x).代入泛函,得,J[y_2]=J[c_1,c_2]=\int_{0}^{1}{[(1-2x)(c_1+C_2x)+c_2x(1-x)]^2-x^2(1-x)^2(c_1+c_2x)^2-2x^2(1-x)(c_1+c_2x)}dx. 将J[y_2]分别对c_1和c_2求偏导,然后令{\partial J\over \partial c_1}=0,{\partial J\over \partial c_2}=0, 得方程组,\left\{\begin{array}{ll}\\{3 \over 10}c_1+{3 \over 20}c_2={1 \over 12}\\{3 \over 20}c_1+{13 \over 105}c_2={1 \over 20}\end{array}\right.
解此方程组,得c_1={71 \over 369},c_2={7 \over 41}, 故二级近似解为,f_2={1 \over 41}x(1-x)({71 \over 9}+7x).
- 近似解与精确解的比较.
通过解Euler方程,可得变分问题的精确解为,y={sinx \over sin1}-x. 现将精确解,一级近似解,二级近似解比较如下:
| Z | 精确解 | 一级近似解 | 二级近似解 |
|---|---|---|---|
| y={sinx \over sin1}-x | y_1={5 \over 18}x(1-x) | f_2={1\over41}x(1-x)({71\over9}+7x) | |
| 0 | 0 | 0 | 0 |
| 0.2 | 0.0361 | 0.0444 | 0.0362 |
| 0.4 | 0.0627 | 0.0667 | 0.0626 |
| 0.6 | 0.0710 | 0.0667 | 0.0709 |
| 0.8 | 0.0525 | 0.0444 | 0.0526 |
| 1.0 | 0 | 0 | 0 |
可见,二级近似解与精确解的差已达到10^{-4}数量级。
5.2 康托罗维奇法
对于多元函数的范函J[z(x_1,x_2,…,x_n )],设其可取函数簇的基函数为
u_1 (x_1,…,x_n ) ,u_2 (x_1,…,x_n ),…,u_m (x_1,…,x_n ),…
用Ritz法求解这种形式的变分问题时,变分问题的近似解取成
z_m (x_1,x_2,…,x_n )=∑_(i=1)^m▒〖a_i u_i (x_1,x_2,…,x_n ) 〗
的形式,其中a_i,i=1,2,…,m是待定常数
z_m (x_1,x_2,…,x_n )=z_m (x_1,x_2,…,x_n )=∑_(i=1)^m▒〖a_i (x_k )u_i (x_1,x_2,…,x_n ) 〗
的形式,其中,a_i(x_k),i=1,2,…m,是待定函数。
此时 J[z(x_1,x_2,…,x_n) ]=J ̃[a_1 (x_k),a_2 (x_k),…,a_m (x_k)]
是一个依赖于x_k的m个函数a_1 (x_k),a_2 (x_k),…,a_m (x_k)的范函,求解Euler方程,确定a_i^1) (x_k), 得到原范函函数的m级的近似解。
z ̃_m (x_1,x_2,…,x_n )=∑_(i=1)^m▒〖a_i(x_k)u_i(x_1,x_2,…,x_n) 〗
可以证明,当原范函J[z]满足一定条件时,
lim┬(m→∞)(z_m ) ̃ =z (精确解)
通过讨论范函,
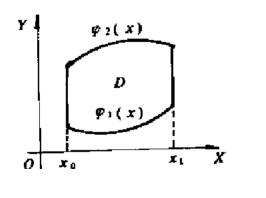
J[z]=∫_(x_0)^(x_1)dx∫_(∅_1(x))^(∅_2(x))F(x,y,z,∂z/∂x,∂z/∂y)dy
在齐次边界条件z(x,y)|∂D=0下的极值问题,如下图,说明康氏法的步骤。
主要有3个步骤:
1. 选取可取函数簇Y的基函数,确定$m$
$u_1(x,y), u_2(x,y),…,u_m (x,y),…$ 确定$m$,
作$z_m (x,y)= \sum_(i=1)^m {a_i(x) u_i(x,y)} \in Y$
2. 计算 $J|z_m|$
3. 将J̃[a_1,a_2,…,a_m]看成是a_i(x), i=1,2...m 的范函, 选取a_i(x),
使J[a_1,a_2,…,a_m]取极值,极值函数a_i应满足J ̃ 的欧拉方程组,
∅_(a_i )-d/dx ∅_(a_i )=0, i=1,2,…m
解此方程组,得 a_i^((m) ) (x), i=1,2...m,d代入z_m,得m级近似解
z ̃_m (x,y)=∑_(i=1)^m a_i^m(x)u_i(x,y).
5.3 求解变分问题的有限元法
目的:
* 利用变分法求解偏微分方程
* 学习直接求解变分问题的有限元方法
摘要:
三维数据采样设备的长足进步使网格参数化成为了逆向工程的研究重点和热点。然而现有的参数化方法难以保证参数域是矩形的切参数曲线网是正则的。为克服局限性,本文提出新颖的参数化方法。其基本思想第一是基于稳态温度场中等温线的均匀分布与不相交,保证参数化不存在奇异情况;第二是对四边三角网格曲面,用有限元素法求解一个三维调和方程,来得到二维曲面上的稳态温度场,完全避免了没有网格顶点参数值,求解二维拟调和方程的困境。以温度场的等温线作为曲面的一族等参线,再连接等温线上弧长间隔相同的点得到另一族等参线,由此得到的参数曲线网必然正则且分布均匀,可将四边三角网格曲面映射到单位矩阵参数域,且曲面边界映射到参数域边界,从而确保用NUBRS曲面来拟合三角网格曲面或点云的顺利实现。
将空间三角网格顶点,映射到平面上,每个顶点得到两个参 数值。在网格拟合中,两参数形成的两族参数网格线,必须 是正则的。
范围无限的稳态温度场中的两族曲线,等温线和温度的最速降线,是相互正交的。它们可以作为网格曲面上的两族参数线,将网格顶点参数化 。
方法:
网格顶点在空间中有三个坐标(x,y,z),因此,网格上的稳态温度场满足三维调和方程
我们需要把面变成体,我们将网格曲面S的顶点沿其法向移动一个小距离,顶点之间的 连接关系不便,得到一张等距网格曲面U,连接两张曲面相应的顶点,得到一个体V, 原来的网格曲面S是体的一个底面。计算出这个体中的稳态温度场,就得到了原网格曲 面上的稳态温度场。
等价问题:
二维偏微分方程等价于变分问题:在集合M中秋函数T(x,y,z),使泛函I(T)取最小值。
用有限元法求解变分问题:
* 区域剖分
对热导体V采样,得到n+m个采样点,n个在V的内部,m个在V的边界B。分别编号为1到n,和n到n+m,将这些点三角化, 得到r个四面体构成的单纯复形,编号为1到r个编号。相当于将V中每个三棱柱剖分为两个四面体。
* 在每个四面体上构造线性插值函数.
四面体中任意一点 P(x,y,z),上的温度值为
* 单元分析,对于每一个四面体构造单元刚度矩阵.
对于第p个四面体Vp,由于
所以,如果记四面体Vp的体积为||Vp||,则
* 总体合成,得到总刚度矩阵
其中
称为总刚度矩阵,由单位刚度矩阵按编号叠加得到。 确定迭代方程组KT=0
* 强加边界条件的处理
由于边界上的温度值是已知的。将上面的方程处理,得到如下的方程组
由于矩阵[kij]n*m是对称正定矩阵,因而上面的方程组一定有解。
本节编撰作者