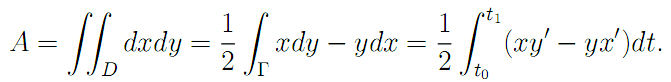Sidebar
Table of Contents
.
第六课 Calculus of Variations(变分法)
6.1 变分概念与变分法基本引理
6.1.1变分法引例
泛函分析是研究拓扑线性空间到拓扑线性空间之间满足各种拓扑和代数条件的映射的分支学科。
泛函的定义域是一个函数集,而值域是实数集或者实数集的一个子集,泛函就是从任意的向量空间到标量的映射。
泛函是从函数空间到数域的映射。
变分学研究的主要内容是泛函的极值。因此,凡是求泛函极值的问题,都可以称作变分问题。
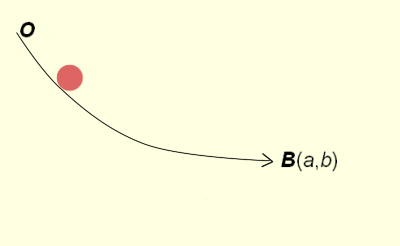
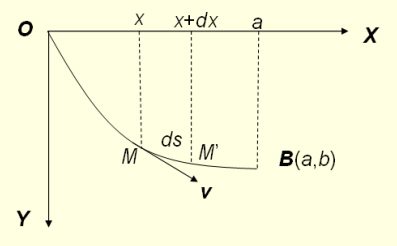
引例1,降线问题 如图所示,小球自由从O点到B点滑落(仅受重力影响),问:当O点与B点之间的曲线是何种轨迹时,小球的滑落时间最{短?
解: ①建立坐标系
②设曲线函数
y=y(x)
③假设在图中N点的速度是v,分析从O到N的过程,根据能量守恒定律,可得:
mgh=1/2mV^2. v=√2gy
④设A为计算曲线弧长的起点,则有
ds/dt=v=√2gy
ds=√(dx^2+dy^2)=√[dx^2(1+dy^2/dx^2)]=dx√(1+y'^2)
故dt=ds/v=[√(1+y'^2)/√(2gy)]dx
⑤从O到B进行积分,总时间
T=∫0→t dt=∫0→a √(1+y^2)/√(2gy) dx
观察上式可以看出,泛函T的值与函数y=y(x)相关,在这种情况下,函数T是无法直接求其极值的。
因此,降线问题最后可以被描述为:求光滑曲线γ : y = y(x), (0 ≤ x ≤ 1),在其满足条件y(0) = 0, y(a) = b下使泛函T[y(x)]取最小值。
引例2,短程线问题 设A(x0,y0,z0)和B(x1,y1,z1)是曲面∑:φ(x,y,z)=0上的两点,求在曲面∑上过A和B的长度为最短的曲线。所求曲线称为短程线或侧地线。
解: 设经过两点的曲线Γ的方程为
y=y(x)
z=z(x) x0≤x≤x1
则曲线Γ的长度为L=∫x0→x1 √(1+y'^2+z'^2)dx
泛函L的值与Γ相关。即L与y = y(x), z = z(x)有关。记L = L[y(x), z(x)],短程线问题可以归结为求曲线
Γ: y=y(x)
z=z(x) x0≤x≤x1
在其满足边界条件y0 = y(x0),z0 = z(x0),y1 = y(x1),z1 = z(x1),及约束条件ϕ(x, y(x), z(x)) = 0下,使泛函L取得最小值。
引例3,等周问题 求长为定值l的平面封闭曲线Γ,使其所围成的平面区域D的面积最大。
解:
设曲线Γ的方程为:
x = x(t),
y = y(t),t0 ≤ t ≤ t1,
由弧长公式知:l=∫t0→t1√(x'^2(t) + y'^2(t))dt
由Green公式,Γ所围成的面积A为
泛函A的值与x(t), y(t)有关。本例的问题归结为在上述条件下使得泛函A取最大值。
引例4,最小旋转面问题 在XOY平面内求一条边界固定的曲线,使其绕着横轴旋转所产生的空间曲面面积最小。
解:
设过点A(x0, y0), B(x1, y1)的曲线方程为y = y(x), x0 ≤ x ≤ x1,
则旋转曲面的面积S为
S = 2π∫x0→x1 y√(1 + y'^2)dx.
泛函S的值与y=y(x)有关,记S=S[y(x)] 于是最小旋转曲面问题归结为:求曲线Y=y(s)(x0≤x≤x1)在其满足边界条件
y(x0)=y0,y(x1)=y1
下面使泛函S取极小值
引例5,悬链形状问题 求长度为l两段系于A和B两点,绝对柔软而不伸长的匀质链的形状。
解: 设链的方程y = y(x), (0 ≤ x ≤ x1),链的线密度ρ,按照位能原理,链的形状应该使链具有最小位能。
小弧段ds的位能为:dU = ρds ˙ gy = ρgy√(1 + y'^2)dx
链的总位能为:U = ρg∫y√(1+y'^2)dx
泛函U的值与曲线y=y(x)有关。记PU = U[y(x)],于是悬链问题归结为在上述条件下求泛函U的极小值。
综上可以看出共通点:
①这些例子都是求泛函的极值问题。
②边界都是固定的,端点有不变的值。
③除边界条件外,有些再无其他条件,有些则另外有附加条件。有的条件是一般函数,有的条件也是泛函。其中,固定边界且无条件的泛函是最基本最简单的泛函。
6.1.2 变分概念与引理
变分问题即泛函的极值问题。
1.变分概念
定义1:
设 J[y(x)] 是定义在函数集合Y = { y(x) } 上的泛函,称 y(x) 为 J[y(x)] 的宗量,Y 是 J[y(x)] 的定义域(或容许曲线类(簇))。
引例1中,J[y(x)] = \int_0^1 y(x) dx是定义在Y = \left\{y(x), y(x) \in C[0,1]\right\}上的泛函,y(x) 是该泛函的宗量,Y 为容许曲线簇。
通俗地理解,宗量即自变量,为了与函数定义中的自变量区分开来引入的概念,在讨论泛函的连续以及其他性质时需要此概念。宗量和容许曲线簇之间没有区别,都是指泛函的自变量。
定义2: 泛函 J[y(x)] 的宗量与另一宗量y_0(x)之差,称为宗量 y(x) 的变分,记为 δy = δy(x) = y(x) - y_0(x).
定义3:
若max|y(x)-y_0(x)|很小,则称 y(x) 与y_0(x)具有零阶接近,称函数集合\{ {y(x)} | {|y(x)-y_0(x)| < δ} \} 为 y_0(x) 的零阶 δ- 邻域。
设 k 为正整数,若max\{ |y(x)-y_0(x)|, |y'(x)-y_0'(x)|,…,|y^{k}(x)-y_0^{k}(x)| \}很小,则称 y(x) 与y_0(x)有k阶接近,称函数集合
定义4: 如果 ∀ε > 0,使对y_0(x)的 k 阶 δ- 邻域中的任何y(x),都有| J[y(x)]-J[y_0(x)]| < ε,则称 J[y(x)] 是在y_0(x)处具有 k 阶接近度的连续泛函。
定义5: 设 F(x, y, y') 是关于三个变元 x, y, y' 的二阶连续可微函数,x 任意固定,η(x) 是任意可微函数,ε 是无穷小参数,则 F(x, y, y') 的增量为
并且满足δ(F_1 + F_2) = δF_1 + δF_2和δF_1F_2 = F_1δF_2 + F_2δF_1
定义6(泛函的变分第一种定义): 如果 J[y(x)] 的增量 ΔJ = J[y + δy] - J[y] 可以表示为
定义7(泛函的变分较弱的定义): 考虑含参数 α 的一系列容许曲线 y(x)+ αδy,将 y(x),δy 任意固定,泛函 J[y+ αδy] 看成是参数 α 的函数,记为Φ(α) = J[y+ αδy]。如果Φ'(0) = \frac{∂}{∂α}J[y+ αδy]|_{α=0}存在,则称 Φ'(0) 为泛函 J[y] 的变分,仍记为 δJ,即
定理1. 对于泛函 J[y] ,若按定义 6 的变分存在,则在定义 7 意义下 J[y] 的变分也存在并且两者相等.
变分问题转换为泛函的一阶求导
定义8:
设y_0(x)是泛函 J[y] 的容许曲线簇 Y 中的某一函数,若对 ∀y ∈ Y,都有J[y(x)] ≤ J[y_0(x)](或J[y(x)] ≥ J[y_0(x)]),则称泛函 J[y] 在y_0(x)处达到极大(小)值(或绝对极大(小)值),并称y_0(x)为 J[y] 的极大(小)值曲线.
若对于y_0(x)的零阶 δ- 邻域内的所有函数 y(x), 都有J[y(x)] ≤ J[y_0(x)](或J[y(x)] ≥ J[y_0(x)]),则称泛函 J[y] 在y_0(x)处达到强极大(小)值.
若对于y_0(x)的一阶 δ-邻域内的所有函数 y(x),都有J[y(x)]≤J[y_0(x)](或J[y(x)]≥J[y_0(x)]),则称泛函 J[y] 在y_0(x)处达到弱极大(小)值,此时y_0(x)是 J[y]的极大(小)值曲线。
推论2 绝对极值必是强极值.
推论3 泛函 J[y] 达到绝对极值的必要条件也是达到弱极值的必要条件,更是达到强极值的必要条件.
证明.Φ(α) = J[y_0(x) + αδy]在 α = 0 时达到极值,故 Φ'(0) = 0. 即δJ[y_0(x)] = 0.
6.1.3 变分法基本引理
1.基本引理1. 设 Φ(x) ∈ C[x_0, x_1],如果对∀η(x) ∈ C'[x_0, x_1], η(x_0) = η(x_1) = 0,都有
证明:恒等于风格的问题使用反证法
假设 Φ(x) 在[x_0, x_1]中的某点 ξ 处不等于0,不妨设Φ(ξ) > 0. 由 Φ(x) 的连续性知,必存在区间[ξ_0, ξ_1],使 ξ ∈ [ξ_0, ξ_1] ⊂ [x_0, x_1],并且当 x ∈ [ξ_0, ξ_1] 时,Φ(x) > 0. 此时η(x)的取值情况如下:
*当x_0 ≤ x ≤ ξ_0时,η(x) = 0.
*当ξ_0 ≤ x ≤ ξ_1时,η(x) = (x - ξ_0)^2(x - ξ_1)^2.
*当ξ_1 ≤ x ≤ x_0时,η(x) = 0.
则η(x_0) = η(x_1) = 0,η'(x) 在[x_0, x_1]上连续,即 η(x) 适合引理1的条件,但是
2 基本引理2. 设 D 为平面区域,D 的边界为 Γ,Φ(x,y) ∈ C(D), 若对任一在 D + Γ 上连续可微且在 Γ 上取零值的函数 η(x,y), 都有
证明: 用反证法。假设 ∃(ξ,ξ) ∈ D,使 Φ(ξ,ξ) ≠ 0,不妨设 Φ(ξ,ξ) > 0. 由 Φ(x,y) 的连续性知,∃ρ > 0, 使 Φ(x,y) 在圆S_ρ: (x - ξ)^2 + (y - ξ)^2 < ρ内仍为正,且S_ρ ⊂ D。构造函数:
*当(x - ξ)^2(y - ξ)^2 ≥ ρ^2时,η(x,y) = 0.
*当(x - ξ)^2(y - ξ)^2 < ρ^2时,η(x,y) = [(x - ξ)^2 + (y - ξ)^2 - ρ^2]^2.
函数 η(x,y) ∈ C^1(D), 且 η(x,y)|_Γ = 0. 但是:
6.2 固定边界的变分问题
6.2.1 泛函极值的必要条件与Euler方程
- 泛函极值的必要条件
最简单的泛函的极值问题:
J[y(x)]= \int_{x_0}^{x_1} {F(x,y,y')dx,} (5)
其中,F∈C^2,容许曲线y(x)∈C^2[x_0,x_1],且满足边界条件:
y(x_0)=y_0, y(x_1)=y_1. (6)
极值的必要条件:使泛函J[y]=\int_{x_0}^{x_1} {F(x,y,y')dx}达到极值的必要条件,是y(x)满足Euler方程:
F_y- \frac{d}{dx}F_y=0. (7)
证明:构造以α为参数的容许曲线族\overline {y}(\alpha )=y(x)+\alpha \delta y,
其中,\delta y为宗量y(x)的变分,满足\delta y|_{x=x_0}=\delta y|_{x=x_1}=0.
所以,\overline {y}|_{x=x_0}=y_0,\overline {y}|_{x=x_1}=y_1,\overline {y}\in C^2[x_0,x_1].
假设,当α=0时,\overline {y}=y(x)是使泛函(18)达到极值的曲线,将\overline {y}代入方程(18),得到
\Phi (\alpha )=J[y+\alpha \delta y]=\int_{x_0}^{x_1} {F(x,y+\alpha \delta y,y'+\alpha \delta y')dx.}
由于\Phi (\alpha )在α=0时取得极值,由极值的必要条件,有
\Phi '(0)=\frac{\partial }{\partial \alpha }J[y+\alpha \delta y]|_{\alpha =0}=\int_{x_0}^{x_1} {(F_y\delta y+F_y\delta y')dx}=0. (8)
由分部积分法,并注意到\delta y|_{x=x_0}=\delta y|_{x=x_1}=0,有
\int_{x_0}^{x_1} {F_{y'}}\delta y'dx=\int_{x_0}^{x_1} {F_{y'}}d(\delta y)=F_{y'}\delta y|_{x_0}^{x_1}-\int_{x_0}^{x_1} {\delta y\frac{d}{dx}F_{y'}dx}=-\int_{x_0}^{x_1} {\delta y\frac{d}{dx}F_{y'}dx}.
将上式代入方程(8),得到
\Phi '(0)=\delta J=\int_{x_0}^{x_1} {[F_y-\frac{d}{dx}F_{y'}]\delta ydx}=0.
由基本引理1知,使泛函J[y]达到极值的函数y(x)必满足Euler方程7.
说明:注意到满足Euler方程7仅是泛函取到极值的必要条件,Euler方程7的解曲线仅仅是可能的极值曲线。但是,在实际问题中,往往可以事先确定泛函的极值是否存在。在确定了极值存在的情况下,Euler方程的解曲线就是极值曲线.
6.2.2 含有多个未知函数的变分问题
- 含两个未知函数的泛函极值的必要条件
☆问题:
J[y(x),z(x)]=\int_{x_0}^{x_1}{F(x,y,z,y',z')}dx, (11)
其中,F关于所含变量具有二阶连续领导,容许曲线y(x),z(x)∈C^2[x_0,x_1],且满足边界条件:
\left\{ {\begin{array}\ {y(x_0)=y_0, y(x_1)=y_1,}
{z(x_0)=z_0, z(x_1)=z_1}.
\end{array} } \right.
☆极值的必要条件:使泛函J[y(x),z(x)]=\int_{x_0}^{x_1}{F(x,y,z,y',z')}dx达到极值的必要条件是,y(x),z(x)满足Eular方程组,即:
\left\{ {\begin{array}\ {F_y-\frac{d}{dx}F_{y'}=0,}
{F_z-\frac{d}{dx}F_{z'}=0}.
\end{array} } \right. (12)
☆例1.求泛函J[y,z]=\int_{0}^{\frac{π}{2}{(y'^2+z'^2+2yz)}}dx满足边界条件:
\left\{ {\begin{array}\ {y(x_0)=0, y(\frac{π}{2})=1,}
{z(x_0)=0, z(\frac{π}{2})=-1}.
\end{array} } \right.
的极值曲线。
解:F=y'^2+z'^2+2yz,故Eular方程组为:
\left\{ {\begin{array}\ {2z-\frac{d}{dx}(2y')=0,}
{2y-\frac{d}{dx}(2z')=0}.
\end{array} } \right.
得:
\left\{ {\begin{array}\ {z-y^{(2)}=0,}
{y-z^{(2)}=0}.
\end{array} } \right.
由此方程组消去z,得y^{(4)}-y=0,其通解为:
\left\{ {\begin{array}\ {y=c_1e^x+c_2e^{-x}+c_3cosx+c_4sinx,}
{z=y''=c_1e^x+c_2e^{-x}-c_3cosx-c_4sinx}.
\end{array} } \right.
由边界条件可确定c_1=c_2=c_3=0,c_4=1,故,所求极值曲线为:
\left\{ {\begin{array}\ {y=sinx,}
{z=-sinx}.
\end{array} } \right.
★例2 求泛函J[y(x),z(x)]=\int_{x_0}^{x_1}{F(y',z')dx,} 的极值曲线,其中假设 F_{y'y'}-F^2_{y'z'} ≠0
解:因为F_y=F_z=0,故Euler方程组为
\left\{ {\begin{array}\ {\frac{d}{dx}(F_{y'})=0,}
{\frac{d}{dx}(F_{z'})=0}.
\end{array} } \right.
得:
\left\{ {\begin{array}\ {F_{y'y'}y“+F_{y'z'}z”=0,}
{F_{y'z'}y“+F_{z'z'}z”=0}.
\end{array} } \right.
根据假设条件,该方程只有零解y“=0,z”=0,即
\left\{ {\begin{array}\ {y=c_1x+c_2,}
{z=c_3x+c_4}.
\end{array} } \right.
是所求的极值曲线。
- 含n(n>2)个未知函数的泛函极值的必要条件
泛函J=\int_{x_0}^{x_1}{F(x,y_1,y_2,…,y_n,y'_1,y'_2,…y'_n)dx,}在满足边界条件
\left\{ {\begin{array}\ {y_i(x_0)=y_{i0},}
{y_i(x_1)=y_{i1}},i=1,2,…n,
\end{array} } \right.
下,取得极值的必要条件是y_1(x),y_2(x),…,y_n(x),满足Euler方程组
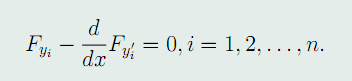
上述方程组通解中的常数,可以由所给的边界条件确定。
![]()
6.3 可动边界的变分问题
6.3.1 最简单的可动边界问题
固定边界的变分问题:在未知函数 y(x) 的边界点A(x_0, y_0), B(x_1, y_1)固定的情况下,求泛函J[y(x)] = \int_{x_0}^{x_1}F(x,y,y')dx的极值曲线。
当两边界点中的一个或两个是可以变动的 → 可动边界的问题。可动边界情况下的容许曲线簇是包含固定边界情况下的容许曲线簇。因此,当函数 y(x) 使可动边界的泛函达到极值,也能够使固定边界的泛函达到极值。此时的求解条件为:
1. Euler方程F_y - \frac{d}{dx}F_{y'} = 0.
2. 斜截条件.
斜截条件:
y(x)有一个固定的左端点A(x_0, y_0),右端点B(x_1, y_1)在某曲线 ω(x, y) = 0上移动。考察x_1满足的特征.
考察当右边界点B(x_1, y_1)移动到\bar{B}(x_1+δx_1, y_1+δy_1)的时,泛函 J 的增量为

如上图所示,δy_1是当边界点移到(x_1+δx_1, y_1+δy_1)位置时y_1的增量,δy|_{x=x_1}是当通过(x_0, y_0)和(x_1, y_1)两点的极值曲线移到通过(x_0, y_0)和(x_1+δx_1, y_1+δy_1)两点的极值曲线时,在点x_1处纵坐标的增量。
在图中, BD = δy|_{x=x_1}, FB' = δy_1, EB'\approx{y'(x_1)δx_1},所以 BD = FB' - EB',即δy|_{x=x_1} \approx{δy_1 - y'(x_1)δx_1}。此时,近似等式与精确等式相差一个较δx_1高阶的无穷小量,将(22)式代入(21)式得到:
如果δx_1和δy_1无关 → (F - y'F_{y'})|_{x=x_1} = 0, F_{y'}|_{x=x_1}=0. —(25)
如果δx_1和δy_1相关,设右端点沿某一曲线C_1: w(x, y)=0移动,此时有 ω_{x_1}δx_1 + ω_{y_1}δy_1 = 0. —(26)
假设ω_{y_1} ≠ 0,, δy_1 = -\frac{ω_{x_1}δx_1}{ω_{y_1}}.
代入(24)式有,[(F - y'F_{y'})ω_{y} - F_{y'}ω_{x}]|_{x=x_1} = 0. —(27)
(27)时为斜截条件(贯截条件)。表明当 y = y(x), (x_0 ≤ x ≤ x_1)为变动右端点的泛函极值曲线,则右端点满足此式子。
* 右端点 B 可以沿曲线C_1: y = φ(x)移动,此时有ω = y - φ(x),ω_x = -φ'(x), ω_y = 1; 斜截条件为:[(φ'(x)-y')F_{y'} + F]|_{x=x_1}.
* 右端点 B 可以沿直线 x = x_1上移动,此时称 B 为自由端点,而δx_1 = 0. 斜截条件成为: F_{y'} | {x=x_1} = 0. 表示F_{y'}沿着 y = y(x)在 x = x_1处的值为零。此时的斜截条件也称为 J[y] 的自然边界条件.
* 右边界点B在直线 y = y_1上移动,于是δy_1 = 0. 斜截条件为: [F - y'F_{y'}] = 0.
当左右边界均可动时可以推导出相应的斜截条件.
例2.
求联结平面上两条曲线 x + y + 1 = 0 与 xy = 1 的最短曲线.
解:
设所求平面曲线为 y = y(x),现求泛函 J[y] = \int_{x_0}^{x_1}\sqrt{1 + {y'}^2}dx的极值曲线,且,两个端点A和B都是变动的:

解上述方程得到: x_0 = -\frac{1}{2}, x_1 = 1, c_1 = 1, c_2 = 0.
若x > 0,那么所求曲线为 y = x, (-1/2 ≤ x ≤1)。
- 王礼文 (ID: 11021035), 编写了…
- AuthorName2 (ID: xxxxxxxxx), 编写了…
- 冉清 (ID: 11021038), 编写了6.1.2变分概念和基本问题.6.3.1最简单的可动边界问题
- AuthorName3 (ID: xxxxxxxxx), 编写了…
- 张娜 (ID: 11021040), 编写了6.1变分法引例
- 徐磊 (ID: 11021041), 编写了6.2固定边界的变分问题
浙江大学2008-2010版权所有,如需转载或引用,请与 作者联系。