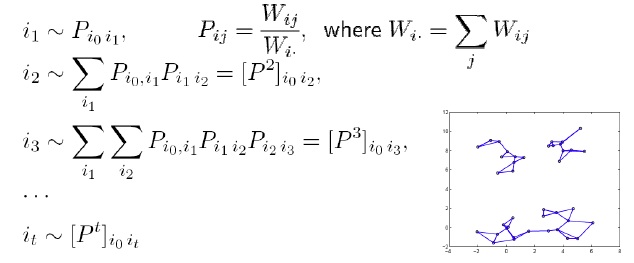Sidebar
keynote:2011-lesson03
第三课
Distance and similarity
- Clustering: unsupervised method to group data points, and find the overall structure.
- Distance : L^1 distance, L^2 distance, L^p distance.
- Distance, Norm and inner procuct.
- Dimensional aware distances.
- M-distance: dist(x,y;M)=(x-y)^{T}M^{-1}(x-y)
- More complex methods: PCA, MDS, LLE.
- Isomap: use the geodesic distances on manifold between all pairs.
- Three step algorithm:
- Using KNN or \varepsilon -radius distance to construct neighborhood graph.
- Using Floyd's algorithm to compute the shortest paths between every pair of nodes.
- Minimize the cost function to construct d-dimensional embedding.
- Application:
- Texture mapping.
- Face Detection.
- LLE: locally linear embedding, recovers global nonlinear structure from locally linear fits.
- Main idea: represent each data point as a weight-sum function of its neighbour point.
- Input: D dimension data.
- Output: d<D dimension data.
- Three step algorithm:
- Find the neighbour point of each data point.
- Minimize a reconstruct error function with normalize constrains to decide the neighbour weights.
- Find embedded coordinates by minize a global reconstruct error energy function with constrains.
- Spectral clusterging
- Main idea:relies on a random walk representation over the points
- Algorithm consists of three steps
- a nearest neighbor graph
- similarity weights on the edges
- transition probablility matrix
- properties of the random walk
- if we start from i0 the distribution of points it that we end up in agter t steps is given by
- K-means clusterging
- Main idea: The main idea is to define k centroids, one for each cluster. These centroids shoud be placed in a cunning way because of different location causes different result.
- Algorithm consists of the following steps
- 1. Place K points into the space represented by the objects that are being clustered. These points represent initial group centroids.
- 2. Assign each object to the group that has the closest centroid.
- 3. When all objects have been assigned, recalculate the positions of the K centroids.
- 4. Repeat Steps 2 and 3 until the centroids no longer move. This produces a separation of the objects into groups from which the metric to be minimized can be calculated.
- Remarks
- Although it can be proved that the procedure will always terminate, the k-means algorithm does not necessarily find the most optimal configuration, corresponding to the global objective function minimum. The algorithm is also significantly sensitive to the initial randomly selected cluster centres. The k-means algorithm can be run multiple times to reduce this effect.
- K-means is a simple algorithm that has been adapted to many problem domains. As we are going to see, it is a good candidate for extension to work with fuzzy feature vectors.
- 高斯混合模型 Gaussian Mixture Model
- 如果 p(x | \theta_m) 是多元正太分布,即高斯分布,则此混合聚类的模型即为高斯混合模型(GMM)。在高斯混合模型中,\theta_m = {\{\mu_m, \sum_m}\},其中\mu_m表示第m个成分的均值,\sum_m表示第m个成分的协方差。其中,概率密度函数可以表示为:
- p(x|\theta_m)=p(x|\mu_m,\sum_m) = \frac{exp\{-1/2(x-\mu_m)^T\sum_m^{-1}(x-\mu_m)\}}{(2\pi)^{d/2}|\sum_m|^{1/2}}
- 具体来说,GMM 假设数据是服从一个混合高斯分布,也就是许多个独立的高斯模型的加权,聚类的过程实际上就是对这个 model 进行 fitting 的过程,恢复出各个高斯模型的参数之后,每个数据点属于该类别的概率也就很自然地使用该高斯模型生成这个数据的概率来表示了。通常我们都使用最大似然的方式来对概率模型进行 fitting ,但是混合高斯模型由于对多个高斯分布进行加权,结果的概率式子很难解析地或者直接地求得最大似然的解,所以在计算的过程中采用了分布迭代的过程,具体是使用了一种叫做 Expectation Maximization (EM) 的方法,进行迭代求解。
- GMM 有一些缺点,比如有时候其中一个 Gaussian component 可能会被 fit 到一个很小的范围内的点或者甚至单个数据点上,这种情况被称作 degeneration ,这个时候该模型的协方差矩阵会很小,而那里的概率值会变得非常大甚至趋向于无穷,这样一来我们可以得到极大的似然值,但是这样的情况通常并没有什么实际用处。解决办法通常是给模型参数加上一些先验约束,或者显式地检测和消除 degeneration 的情况。
本节编撰作者(请大家在这里报到):
- 刘霄 (ID: 11021018), 编写了LLE、Isomap以及之前的内容
- 林云胤 (ID: 11021017), 编写了spectral clustering
- 黄龙涛 (ID: 11021014), 编写了K-means clusterging
- 雷昊 (ID: 11021015), 编写了GMM高斯混合模型
- AuthorName5 (ID: xxxxxxxxx), 编写了…
- AuthorName6 (ID: xxxxxxxxx), 编写了…
浙江大学2008-2010版权所有,如需转载或引用,请与 作者联系。
keynote/2011-lesson03.txt · Last modified: 2023/08/19 21:02 (external edit)
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 4.0 International