Sidebar
keynote:2011-lesson01
Table of Contents
第一部分 多变元分析(Multivariate Analysis)
课程初始化
每周四: 6:30-9:30
- 春:论文+平时
- 夏:论文+平时+考试
教师
- 张宏鑫(CAD&CG) Tel: 88206681 ext 518
- 蔺宏伟(CAD&CG) Tel: 88206681
网站 http://www.cad.zju.edu.cn/home/zhx/csmath/doku.php?id=2011
- 作业
- 用wiki完成课堂笔记
- 不定期的课堂小作业
- Python
- 内容
- 多元统计方法
- 非线性优化求解
- 偏微分方程
- 应用泛函方法
参考书
- Pattern Classification
- 最优化理论和方法
- Level set methods and dynamic implicit surfaces
- Functional Analysis (2nd ed.)
更多参考书
- Course paper
- English or Chinese
- Latex
- 学号.姓名.春.pdf
- Mail, 注明姓名、学号
课程小报告
- 最新学术论文中的数学方法
- 代替读书报告
引言: 数据驱动
大纲
- 背景
- 什么是数据驱动
- 数据驱动对于计算机科学和技术有何帮助
当今计算机科学最大的现状和挑战
- 大量企业正在收集数据:
- Google, Apple, Facebook, IBM, Microsoft, Amazon, …
- 中国: 3Q War, Taobao, Sina, Baidu
- 数据,数据,数据……
- 需要大量乏味的重复的工作才能创建数字化的世界
- 需要寻找新的交互方式,创造新类型的媒体
- 花费高的代价才能请专家(科学家、工程师、电影制作人员、图形设计师、优秀艺术家和游戏设计人员)来完成工作
- 需要高效地处理已经存在的数据,并通过它们获得新的数据
计算机是高效运行的机器
- 各种图像、场景,只要人能够创造,就可以利用计算机来得到它
- 但是如何来创造这些图像、场景
完全过程化合成VS完全数据化
- 为电影中的一个角色创造动作
- 完全过程化合成
- 动作比较连贯,但是很容易让人觉得是伪造的,很少在实际中这样用
- 完全手工制作或者完全数据化
- 效果质量很高,但是连贯性不好
- 把两者结合起来的混合方法或许是最好的!?
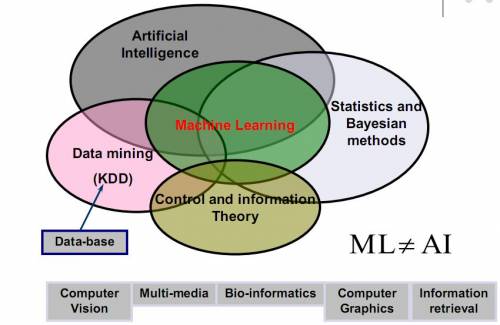
贝叶斯推理
- 关于不确定性的一个规则模型
- 非结构化数据的通用模型
- 数据拟合和不确定分析的有效算法
但是,当前它通常被当做一个黑盒来使用
确定性 VS 机率性
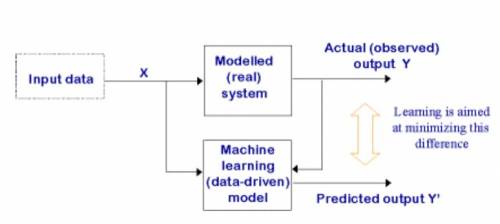
数据驱动模型
数据驱动相关技术
- 学习系统不只是用来解决一个问题,而是基于一些特征来使系统本身更加优化:
- 关于系统应该如何做出响应的一些例子
- 关于系统在解决问题的过程中反复试验学习到的经验
- 不同于通常的计算机科学,去实现一个未知的功能;仅仅是处理已知的输入输出数据对(学习过程中的训练例子)
学习问题的主要分类
- 学习情景根据训练例子中提供的有效信息的改变而改变
- 监督的:需要正确的输出
- 分类:输入N个目标,输出结果为选择其中一个(语音识别、目标辨认、医学诊断)
- 回归:输出准确值(预测未来的市场价格、温度)
- 部分监督的:只输出一部分有效结果
- 无监督的:没有反馈,需要对输出进行自我评估
- 聚类:聚类是指将数据分割成连贯的群集的技术
- 结构异常识别:检测超出正常范围的数据点
- 加强的:标量反馈,可能暂时推迟
更多
- 时间序列分析
- 降维
- 模型选择
- 泛型方法
- 图形建模
为什么学习数据驱动有用?
- 开发强化的计算机系统
- 能够自动适应用户,更加符合用户要求
- 旧的系统往往很难获得必要的知识
- 发掘大型数据库中离线的新数据挖掘模式
- 提高对人的认识,生物学习
- 提供具体的理论计算分析,预测
- 分析大脑的学习过程中的爆发式活动
- 研究时机很好
- 数据量的快速增长
- 计算机不再昂贵而且功能强大
- 理论得到了很好的发展,有一系列的算法组件
对计算机科学和技术有用吗?
- 赞成方:所有事物都是机器学习,所有事物都是人的调整
- 在有些时候,这个说法是正确的
- 反对方:虽然是对“学习”的一种深化,但还有其它更强大和有效的算法。
- 问题分类
- 通用模型
- 通过概率进行推算
- 相信数学的魔力
怎样才是一个成功的学习算法?
- 计算效率
- 鲁棒性
- 统计稳定性
一些实际应用
- Google!
- 目标识别和辨认——学习的力量
- 文档处理——贝叶斯分类器
- 网格处理——数据聚类和分割
- 纹理合成和分析——隐式马尔科夫模型
- 反射纹理合成——降维
- 人体建模——降维
- 图像处理和合成——图形建模
- 人体运动合成——时间序列分析
- 视频纹理——强化学习
总结
- 学习系统就是这样看上去很难但非常有用的东西

- 关键字:
- 名词:数据、模型、模式、特征
- 形容词:概率性的、统计的
- 动词:拟合、推理、挖掘
作业
- 在你的研究方向上寻找学习系统的潜在应用
参考文献
引言: 点估计
主成分分析(Component Analysis)
(Felix:11021004 正在用力扩充此部分内容)
Please refer to courseware slides for rich text formula display. Page numbers are appended after references, e.g. [pp.7] denotes page 7 of the current courseware.
引言
From Wikipedia: “Principal components analysis (PCA) finds a set of synthetic variables that summarise the original set. It rotates the axes of variation to give a new set of ordered orthogonal axes that summarize decreasing proportions of the variation.”
原理
给定一个数据集Y, 需要找到一个变换X和一个特征向量W,以期通过W中的变元来描述Y。由于W中的变元是正交的,因此可以滤除Y中原来的变元之间的依赖关系[pp.23]。
- 一个简单的(intuitive)方法是:使用各变元的采样平均(Sample mean)来作为W。 这一方法能够很好地符合Y的分布,这一点可以通过求其二范式来验证[pp.24]。但是,这样一来,通过一个点来代表一个数据集,会带来信息丢失,例如,无法反映数据的离散程度。
- 因此还可以选择使用一条直线来代表Y的分布:x=m+we. 其中m是采样平均,e是代表数据分布的方向向量。通过求取Y的散布矩阵(Scatter matrix)S, 可以发现e是S的最大特征值(Eigenvalue)[pp.27]。
- 在上述方法中继续扩展,可以用一个d维的“平面”代表Y, 即:x=m+w1e1+w2e2+…wded. 注意d比Y的维度M要小得多,因为M维多变元之间可能包含“复合的、非本质”的变元。我们需要找到“本质”的变元,并用一个d维向量来表示[pp.28]。
如何计算
我们使用奇异值分解(Singular Value Decomposition, SVD)来计算主成分,即:X=UDV'. 其中U和V是正交(Orthogonal)矩阵,D是对角(Diagonal)矩阵,使用V'代表V的转置(Transpose)[pp.30].
在实际应用中,需要考虑到样本X的一些特殊情况,例如:
- d»N, 即原有数据集的维数远高于样本数。这种情况可能出现在图像处理中(?求举例)。这时我们转而计算X'的SVD, 即:X'=VDU'. 这样我们只需要计算一个N*N的小矩阵D,而不是d*d的大矩阵D(不确定)[pp.32].
因为统计量是实数,因此可以使用V的转置矩阵(Transpose)来代替V的共轭矩阵(Conjugate transpose)
例子
- PCA在图像压缩中的应用: Comprehensive colourimage normalization
My Abstract of this paper
- What affect an image (scene)
- Lighting geometry
- Illuminant colour
- Image normalization: for image comparison
- To normalization both factors
- Existing process
- Physics, physical characteristics and dependency
- Canceling dependent variables
- Expensive for computing
- Comprehensive normalization
- Feasibility
- Always converge
- Unique convergence (same normalized result)
- Process
- Iteratively perform row(lighting geometry) and column(illuminant colour) normalization until termination condition is met
- PCA和降维
- 使用SVD进行空间变换:Y→W (?求补充)
PCA的问题
- 只适用于正态分布数据(?)
- 推广:ICA, K-PCA, …
距离和相似性(Distance and Similarity)
- 聚类(Clustering):给定一个数据集,对之进行分组,并发现其总体结构。[pp.4]
- 聚类算法是非监督式机器学习(Unsupervised learning)的一种
- 通过聚类可以发现相似性
- n维向量之间的距离(Distance)[pp.5]
- 欧式距离(Euclidian distance): dist(x,y;2)
- 明式距离(Minkowsky distance):dist(x,y;p). 当p=1时,为taxicab distance; 当p=∞时,为Chebyshev距离。
- 距离、范式和内积之间的关系[pp.6]
- M-distance[pp.7]
- 距离的计算
- PCA
- Structure aware
- 思想:对数据集进行映射,在映射后的空间中计算距离
- 方法:[pp.9]
- 多维标度法(MDS)[pp.10]
- 计算样本之间的距离
- 使用SVD寻找相似性
[PAPER] ISOMAP - Isometric feature mapping
- LLE(Locally Linear Embedding)[pp.21]
- 谱聚类(Spectral clustering):利用邻接图和相似度矩阵[pp.29]
- Random walk: 对于一个连通图而言,t步之后的random walk分布与起点无关
- 应用:image segmentation[pp.36]
- 经典聚类算法[pp.38]
- 自底而下:顺序合并最近的点/聚类
- Mixture density estimation[pp.51]
- The Expectation-Maximization algorithm[pp.53]
- K-means clustering[pp.59]
- Mean shift[pp.62]
- 总结
- 距离计算可以用于寻找数据集中合适的相似度标准,并发现本质的数据结构
图模型(Graphical Models)
- 概率性图模型用于对现实世界中的大规模多变元问题进行建模[pp.2]
- 减少变元之间的依赖性(如利用PCA方法)
- 发现变元之间的关系
- 离散随机变量
- 目标[pp.4]
- 参数学习(Parameter learning)
- 推断(Inference)
- 方法
- 非结构化方法[pp.5]
- 贝叶斯网络(Bayesian networks)
- 联合分布(Joint distribution)公式[pp.8]
- 有向无环图(DAG, Directed Acyclic Graph)的概率分布[pp.9]
- 条件独立(Conditional independence)[pp.18]
- Tail-to-Tail
- Head-to-Tail
- Head-to-Head
- 马尔可夫条件(Markov condition)[pp.23]
- 依赖分割(D-separation, Dependence-separation)[pp.24]
- 马尔可夫毯(Markov blanket)[pp.27]
- 马尔可夫网络(Markov network)[pp.28]
- 势函数(Potential function)[pp.30]
- 马尔可夫链(Markov chain)[pp.60]
- 状态空间(State space)
- 初始概率分布(Initial distribution)
- 转移矩阵(Transition matrix)
- 隐式马尔可夫模型(HMM, Hidden Markov Model)
HOMEWORK
- Python programming
- 1-D regression
- Finish the “Gaussian parameters learning”, using google
本节编撰作者(请大家在这里报到):
- 陈龙彪 (ID: 11021004), 编写
- 祁玉 (ID: 11021005), 编写
- 吴双 (ID: 11021006), 编写
- AuthorName4 (ID: xxxxxxxxx), 编写
- AuthorName5 (ID: xxxxxxxxx), 编写
- 骆歆远 (ID: 11021019), 编写
浙江大学2008-2010版权所有,如需转载或引用,请与 作者联系。
keynote/2011-lesson01.txt · Last modified: 2023/08/19 21:02 (external edit)
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 4.0 International