Applied Mathematics for Computer Science

User Tools

Site Tools

You are here: start » keynote » lesson10

Sidebar

CSMATH

keynote:lesson10

This is an old revision of the document!

Table of Contents

第十课 泛函与变分

第一部分 泛函分析

目标：简要地复习在整个课程中将要用到的泛函分析的概念。主要介绍了下面的一些概念
- 函数空间
- 度量空间
- 收敛
- 测度
- 稠子集
- 可分离空间
- 完备度量空间
- 紧致度量空间
- 线性空间
- 线性泛函
- 线性空间的范数和半范数
- 收敛性回顾
- Euclidean空间
- 正交性和基
- Hibert空间
- Delta函数
- 傅立叶变换
- 泛函导数
- 期望
- 大数定律
（定义和概念主要源于Kolmogorov和Fomin的“Introductory Real Analysis”——强烈推荐）

例子

1. R^n是一个n维实数空间，即n元组x=(x_1,…,x_n)，y=(y_1,…,y_n)的集合。如果我们定义点积为

(x,y)=\sum_{i=1}^n x_i y_i
那么我们得到了n维Euclidean空间。R^n中相应的范数和距离是
||x||=\sqrt {\sum_{i=1}^n {x_i}^2}

\rho(x,y)=||x-y||=\sqrt {\sum_{i=1}^n (x_i-y_i)^2}
.
向量
e_1=(1,0,0\ldots0)
e_2=(0,1,0\ldots0)
\cdots
e_n=(0,0,0\ldots1)

构成了R^n中的一个标准正交基。

2. 元素为x=(x_1,x_2,\ldots,x_n,\ldots )，y=(y_1,y_2,\ldots,y_n,\cdots )，\cdots，其中

\sum_{i=0}^{\infty} {x_i}^2 < \infty, \sum_{i=1}^{\infty} {y_i}^2 < \infty，\ldots\ldots

的空间l_2，当使用点积
(x,y)=\sum_{i=1}^{\infty} x_i y_i

时，变为一个无限维的Euclidean空间。

l_2中最简单的标准正交基包括向量

e_1=(1,0,0,0\ldots)
e_2=(0,1,0,0\ldots)
e_3=(0,0,1,0\ldots)
e_4=(0,0,0,1\ldots)
\ldots\ldots\ldots\ldots
存在无限个这样的基。

3. 当包括[a.b]上所有连续函数的空间C_2[a,b]使用点积
(f,g)=\int_a^b f(t) g(t) dt
时，是另一个Euclidean空间的例子。
在这个空间中正交基的一个重要的例子是如下的函数集合
1, \cos \frac{2\pi nt}{b-a}, \sin \frac{2\pi nt}{b-a} (n=1,2,\ldots)

Hibert空间

一个Hibert空间是一个完备的，可分的，并且通常是无限维的Euclidean空间。
一个Hilbert空间是元素f,g,\ldots的集合H，并且对于该集合有
1. H是一个定义标量积的Euclidean空间 2. H对于度量\rho(f,g)=||f-g||是完备的
3. H是可分的（包含一个可数的处处稠密的子集）
4. （通常）H是无限维的
l_1和l_2都是Hilbert空间的例子。

\delta 函数 我们现在考虑返回f \in C在位置t的值的泛函（一个评价泛函）

\Phi [f]=f(t)
注意这个泛函是退化的因为它并不依赖于整个函数f，而只依赖于f在特定位置t的值。
\delta (t)不是一个泛函而是一个分布。
同一泛函可以被写为
\Phi [f]=f(t)=\int_{-\infty}^{\infty} f(s) \delta (s-t)ds
(在L_2中)不存在特性像\delta(t)一样的普通函数，我们可以将\delta(t)看成是一个在t!=0时为零并且在t=0时取无限值的函数。因此有
\int_{-\infty}^{\infty} \delta(t)dt=1

\delta函数可以被看作是一个普通函数序列的极限。例如，如果

r_{\varepsilon}(t)=\frac{1}{\varepsilon}(U(t)-U(t-\varepsilon))
是一个单位面积矩形脉冲，考虑极限
\lim_{\varepsilon \to 0} \int_{-\infty}^{\infty}f(s)r_{\varepsilon}(s-t)ds
由r_{\varepsilon}的定义，因为f是连续的，所有有
\lim_{\varepsilon \to 0}\frac{1}{\varepsilon}\int_{t}^{t+\varepsilon}f(s)ds=f(t)

第二部分 变分法简介

第一章 变分概念与变分法基本引理

变分概念：变分学研究的主要内容是泛函的极值，凡是求泛函极值的问题都称作变分问题。

1 变分问题的几个实例

例1 捷线问题（最速降线问题）
问题：在同一铅直平面内所有连接不在同一铅直线上的O、B两点的曲线中，求一条曲线\Gamma，使初速度为零的质点仅在重力作用下，自较高点O沿\Gamma滑到点B所需时间最短，如图: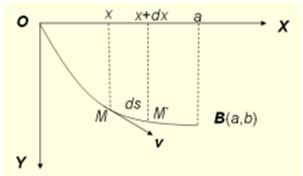eg1
求解思路：利用数学建模写出相应的数学公式；将泛函极值的问题化为相应的欧拉问题；用微分法求解欧拉方程则得到相应的泛函极值。
解：设曲线\Gamma的方程为y＝y(x)，质点质量m，下滑到曲线上点M时获得速度为v，则
由能量守恒、速度的定义与弧长公式分别有：

mgh=\frac{mv^2}{2}；\frac{\mathrm{d}s}{\mathrm{d}t}=v；\mathrm{d}s={\sqrt{1+y'^{2}}}\mathrm{d}x

于是O到B的总时间为如下积分：
T=\int_{0}^{T}\mathrm{d}t=\int_{0}^{a} \frac{\sqrt{1+y'^{2}}}{\sqrt{2gh}} \mathrm{d}x
于是问题归结为：求解泛函T=T[y(x)]，且满足边界条件：y(0)=0,y(a)=b的极值曲线\Gamma

例2 短程线问题
问题：设A(x_0,y_0,z_0)和B(x_1,y_1,z_1)为曲面\Sigma:\phi(x,y,z)=0上的两点，求\Sigma上过A，B的长度最小的曲线\Gamma（也叫测地线）
解：设曲线\Gamma的方程为:

\cases{y=y(x) \\z=z(x) },x_0 \leq x \leq x_1

则曲线\Gamma的弧长为:
L=\int_{x_0}^{x_1} \sqrt{1+y'^{2}+z'^{2}} \mathrm{d}x

于是问题归结为：求解泛函L=L[y(x),z(x)]，中满足边界条件：
\cases{y_0=y(x_0) \\y_1=y(x_1},\cases{z_0=z(x_0) \\z_1=z(x_1}

和约束条件：
\phi(x,y,z)=0

的极值曲线\Gamma：y=y(x),z=z(x)

TanMin谭敏_10921056 tanmin@zju.edu.cn 2010/05/28 21:50

例3 等周问题
问题描述：求长为定值l的平面封闭曲线\Gamma，使其所围成的平面区域D的面积最大.
解：设曲线\Gamma的方程为:

\cases{x=x(t) \\y=y(t) },t_0 \leq x \leq t_1

则封闭曲线\Gamma的弧长为:
l=\int_{t_0}^{t_1} \sqrt{1+x'^{2}(t)+y'^{2}(t)} \mathrm{d}t

由Green公式，\Gamma所围面积A为
A=0.5\int_{t_0}^{t_1} \ {(xy'-yx')} \mathrm{d}t

于是等周问题可以归结为：求一对函数x=x(t),y=y(t)在其满足约束条件
\cases{x(t_0)=x(t_1) \\y(t_0)=y(t_1)}

和等周条件
l=\int_{t_0}^{t_1} \sqrt{1+x'^{2}(t)+y'^{2}(t)} \mathrm{d}t

下使得泛函A取极大值.

例4 最小旋转曲面问题
问题描述：在XOY平面内求一条边界固定的曲线，使其绕横轴旋转所产生的空间曲面面积最小.
解：设过点A(x_0,y_0),B(x_1,y_1)的曲线\Gamma的方程为:

y=y(x),x_0 \leq x \leq x_1

则旋转曲面的面积S为:
S=2\pi \int_{x_0}^{x_1} y{\sqrt{1+y'^{2}}} \mathrm{d}x

记S=S[y(x)].于是，最小旋转曲面问题归结为：求曲线
y=y(x),x_0 \leq x \leq x_1

在其满足约束条件
\cases{y(x_0)=y_0 \\y(x_1)=y_1}

下使泛函S取极小值.
例5 旋链形状问题
问题描述：求长度为l，两端系于A,B亮点，绝对柔软而不伸长的匀质链的形状.
解：设链的方程为
\cases{y=y(x),(t_0 \leq x \leq t_1)}
链的线密度为p,小弧段ds的位能为：
\mathrm{d}U=pgy*ds=pgy{\sqrt{1+y'^{2}}}\mathrm{d}x
链的总位能为：
U=pg\int_{0}^{x_1} y{\sqrt{1+y'^{2}}}\mathrm{d}x

泛函U的值与曲线函数y=y(x)有关，记U=U[y(x)].于是，旋链形状问题归结为：求函数y=y(x)，在其满足条件：
\cases{\int_{0}^{x_1} {\sqrt{1+y'^{2}}}\mathrm{d}x=l,\\y(0)=y_0,
x(0)=x_0,}

下，使得泛函U最小.

2 变分概念

定义1 设J[y(x)]是定义在函数集合Y={y(x)}上的泛函，称y(x)为J[y(x)]的宗量，Y为J[y(x)]得定义域(或许容许曲线类(簇)). 例1设y(x)∈C[0,1],且

J[y(x)]=\int_{0}^{1} y(x)\mathrm{d}x
，试求J[1/(x+1)],J[e^x]及J[1/(1+x^2)].
*解
J[\frac{1}{1+x}]=\int_{0}^{1} \frac{1}{x+1} \mathrm{d}x=In2

L=\int_{x_0}^{x_1} \sqrt{1+y'^{2}+z'^{2}} \mathrm{d}x

J[frac{1}{1+x^2}]=\int_{0}^{1} \frac{1}{1+x^2} \mathrm{d}x=\frac{\pi}{4}

赖攀_10921057 [10921057@zju.edu.cn]

定义6 如果泛函J[y(x)]的增量ΔJ=J[y+δy]-J[y]可表示为:

\ ΔJ=J[y,δy]+β(y,δy)max|δy|,

其中,J[y,δy]对δy是线性的,且δy→0时,β(y,δy)→0,则称J[y,δy]为泛函J[y]的变分,
记作δy,即δy=J[y,δy]。
定义7 如果
Φ’(0)=\frac{\mathrm{∂}}{\mathrm{∂}a}J[y+aδy]|a=0
存在,则称Φ’(0)为泛函J[y]的变分,仍将其记为δJ,即
\ δJ=Φ’(0)=\frac{\mathrm{∂}}{\mathrm{∂}a}J[y+aδy]|a=0

定义8 如设y_0(x)是泛函J[y]的容许曲线簇Y中的某一函数,若对∀y∈Y,都有

\ J[y(x)]≤J[y_0(x) (或J[y(x)]≥J[y_0(x)),

则称泛函J[y]在y_0(x)处达到极大(小)值,(或绝对极大(小)值),并称y_0(x)为J[y]的极大(小)值曲线。
若y_0(x)的 零阶σ–邻域内所有函数y(x)，都有
\ J[y(x)]≤J[y_0(x) (或J[y(x)]≥J[y_0(x)),

则称泛函J[y]在y_0(x)处达到强极大(小)值。
若y_0(x)的 一阶σ–邻域内所有函数y(x)，都有
\ J[y(x)]≤J[y_0(x) (或J[y(x)]≥J[y_0(x)),

则称泛函J[y]在y_0(x)处达到弱极大(小)值。极大(小)值曲线。
推论1 强极值必是弱极值，但反之不真。
推论2 绝对极值必是强极值。
推论3 泛函J[y]达到绝对极值的必要条件也是达到弱极值的必要条件，更是达到强极值的必要条件。

WuXiaoChun吴晓春_10921058 [10921058@zju.edu.cn] 2010/05/31 18:30

keynote/lesson10.1275542025.txt.gz · Last modified: 2023/08/19 21:01 (external edit)

Page Tools

Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 4.0 International
CC Attribution-Noncommercial-Share Alike 4.0 International Donate Powered by PHP Valid HTML5 Valid CSS Driven by DokuWiki counters