Research interests

A. Locality Preserving Projections (LPP) and Manifold Learning

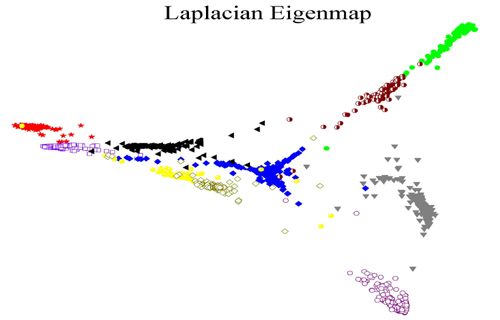
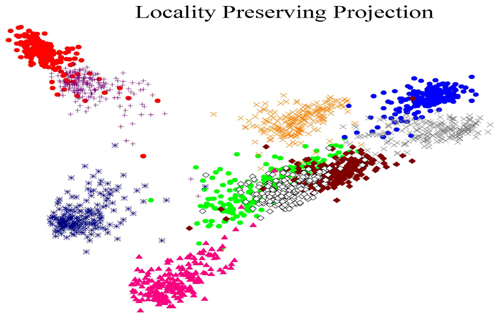
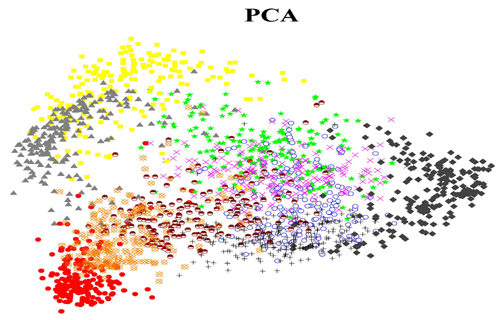
Two dimensional embedding of handwritten digits ("0"-"9") by Laplacian Eigenmap, LPP, and PCA

In many information processing tasks, one is confronted with high-dimensional data. However, the data points are probably sampled from a low-dimensional sub-manifold embedded in the ambient space. I am interested in the general problem: How to learn such a data manifold? Especially, I am interested in the interaction between learning theory and differential geometry.

Working with Prof. Partha Niyogi, we have proposed a novel linear manifold learning algorithm, called Locality Preserving Projections (LPP). LPP is obtained by finding the optimal linear approximations to the eigenfunctions of the Laplace Beltrami operator on the manifold. LPP should be seen as an alternative to Principal Component Analysis (PCA) --- a classical linear technique that projects the data along the directions of maximal variance. When the high dimensional data lies on a low dimensional manifold embedded in the ambient space, the LPPs are obtained by finding the optimal linear approximations to the eigenfunctions of the Laplace Beltrami operator on the manifold. LPP may be conducted in the original space or in the reproducing kernel Hilbert space into which data points are mapped. This gives rise to kernel LPP.

B. Information Retrieval

Design of our image retrieval system, which is equipped with both short- and long-term learning capabilities.

I use information in the broad sense to include text, image, audio, and video. In particular, my research work aloong this direction contains two parts: text retrieval and image retrieval.

 In information retrieval, Latent Semantic Indexing (LSI) is conventionally considered effective for document representation and indexing. LSI essentially detects the most representative features rather than the most discriminant features. Therefore, LSI might not be optimal in discriminating documents with different semantics. Based on LPP, I have proposed a new indexing method called Locality Preserving Indexing (LPI). In contrast to LSI which discovers the global structure of the document space, LPI discovers the local structure and obtains a compact document representation subspace that is optimal for discrimination. If one wishes to retrieval audio, video, text documents under a vector space model, then one will ultimately need to do a nearest neighbor search in the low dimensional space. Since LPI is designed for preserving local structure, it is likely that a nearest neighbor search in the low dimensional space will yield similar (even better) results to that in the high dimensional space. This makes for an indexing scheme that would allow quick retrieval.

 In image retrieval, there are two fundamental problems. First, how to represent an image? Second, how to evaluate the similarity between two images? I tackle these two problems by learning a mapping function from low-level feature space to high-level semantic space. Recently, in joint work with Dr. Wei-Ying Ma and Dr. Hong-Jiang Zhang, I have developed a relevance feedback scheme which is naturally conducted only on the image manifold in question rather than the total ambient space. The geodesic distance on the manifold are used to measure the similarities between images. Based on user interactions in a relevance feedback driven query-by-example system, I designed a long-term learning scheme to estimate the intrinsic similarities between images. I then developed an algorithmic framework to approximate the optimal mapping function by a Radial Basis Function neural network. The semantics of a new image can be inferred by the RBF neural network.

 Besides the retrieval problem, I have also been working on image organization and visualization for efficient browsing. By modeling the image database as a Markov Chain, we have proposed a method to find the most representative images based on the stationary distribution.

C. Web Search and Mining

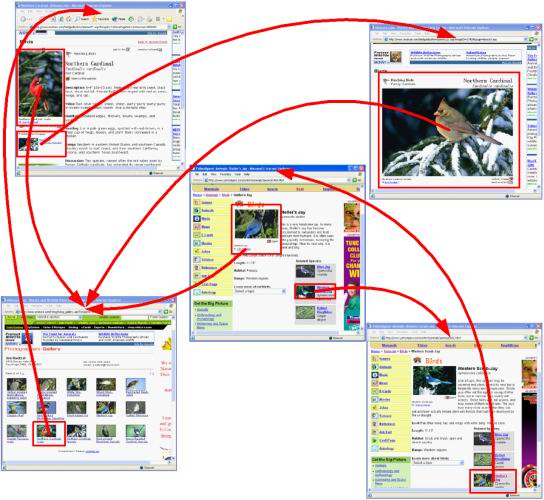Design of our WWW image search system. [more]	The block-to-page link structure. The red arrows denote the links from image block to web pages.

The central question that I ask in my research along this direction is "How to organize the world's information and make it universally accessible and useful?" Specifically, I consider the question: how does a computer see the Internet and web pages?

 The Internet can be naturally represented as a huge graph such that its nodes represent the web pages and its edges represent the hyperlinks. Based on this model, a lot of link analysis algorithms have been proposed to improve the performance of web search. One problem of this model is that the web pages are actually not the smallest information units. In fact, in most cases, a web page can contain various topics and hence the web page might not be considered as the atomic unit. Based on this observation, we have proposed a new link analysis algorithm, called "Block Level Link Analysis". The new algorithm partitions the web pages into blocks. By extracting the page-to-block, block-to-page relationships from link structure and page layout analysis, we can construct a semantic graph over the WWW such that each node exactly represents a single semantic topic.  We further developed two ranking algorithms, block level PageRank and block level HITS.  You can find a lot of comments on this work on the web. Click here!

D. Face Representation and Recognition

The Eigenfaces, Fisherfaces and Laplacianfaces calculated from the face images in the Yale database.

Many research works have shown that the face images lie on a sub-manifold (so called face space)  embedded in the high-dimensional ambient space (image space). I am interested in developing the algorithms for face analysis (detection, representation, and recognition) which explicitly take into account the intrinsic face manifold structure. I am also interested in the problems of face alignment. Recently, in a joint work with Shuicheng Yan, Yuxiao Hu, Partha Niyogi and Hong-Jiang Zhang, I have developed a novel face recognition algorithm called "Laplacianfaces". The new algorithm seeks a linear subspace which can best approximates the non-linear face manifold. Recognition can be then performed much more effectively in such a subspace. We have also shown that the canonical "Eigenface" and "Fisherface" methods can be obtained in our framework by using different graph structures.