最优化方法 4

内容 非线性优化

主要参考书： 最优化理论与方法，袁亚湘，孙文瑜，科学出版社

1.插值法 插值法是一类重要的搜索方法，其基本思想是: 在搜索区间中不断用低次(通常不超过三次)多项式来近似目标函数，并逐步用插值多项式的极小点来逼近一维搜索问题的极小点。当函数具有比较好的解析性质时，插值方法比直接方法(0.618法或Fibonacci法)效果更好。

1.1一点二次插值（牛顿法） 利用一点处的函数值、一阶和二阶导数值构造二次插值函 数.迭代形式：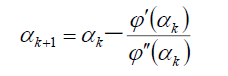

牛顿法的优点是收敛速度快，具有局部二阶收敛速度。

1.2二点二次插值法 给出两点的函数值和其中一点的导数值，构造二次插值函 数。迭代形式为：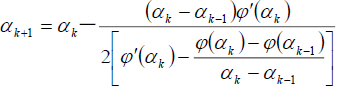

 可证明二点二次插值法的收敛阶为1.618，超线性收敛。

1.3三点二次法（抛物线法）

 迭代时，从α1，α2，α3，α¯中选择目标函数最小的点及其左右两点，

进行下一步的迭代。

 超线性收敛，收敛阶近似为1.32。

1.4二点三次插值法 用三次多项式来逼近。比二次插值法有较好的收敛效果， 但通常要求计算导数值，且计算量较大。一般当导数易求 时，用三次插值法较好。

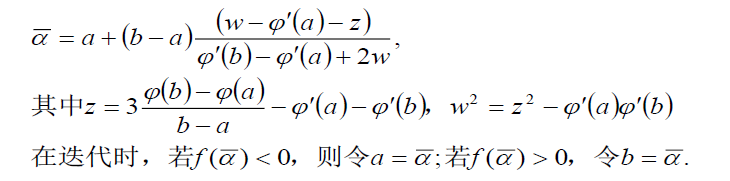
 收敛速度为2阶，一般优于抛物线法。

2.不精确的一维搜索方法

• 精确一维搜索往往需要花费很大的时间。*

当迭代点远离问题的解时，精确求解通常不十分有效。很多最优化方法，如牛顿法和拟牛顿法，其收敛速度并不依赖于精确一维搜索过程。

• 只要保证目标函数有满意的下降，可大大节省计算量。*

2.1Armijo-Goldstein准则 2.2Wolfe-Powell准则  Armijo-Goldstein准则有可能把最优步长因子排除在可接受区间外，因此更改第二个条件为 3.牛顿型方法

3.1最速下降法

• 以负梯度方向作为极小化算法的搜索方向
• 具有总体收敛性
• 最速下降方向仅是局部性质

 对于许多问题并非下降方向，而且下降非常缓慢。接近极小点时，步长越小前进越慢

• 线性收敛

3.2牛顿法

• 牛顿法的基本思想是利用目标函数的二次Taylor展开，并将其极小化。

• 对于正定二次函数，一步即可得最优解。
• 由于目标函数在极点附件近似于二次函数，故在初始点接近极小点时，牛顿法收敛速度较快。
• 牛顿法具有局部收敛性，为二阶收敛。

3.3改进牛顿法 牛顿法的主要困难在于Hesse阵Gk不正定。这时二次型模型不一定有极小点，甚至没有平稳点。 Goldstein and Price (1967)当Gk非正定时，采用最速下降方向结合方向，给出

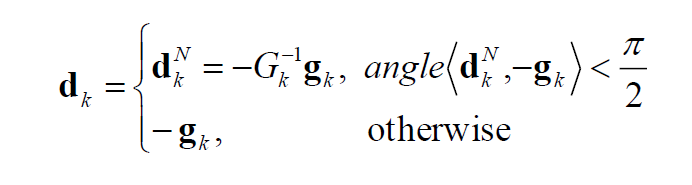3.3.1Goldfeld修正牛顿法 3.3.2Gill-Murray稳定牛顿法 3.3.3Levenberg-Marquardt方法 3.3.4信赖域方法

• 不仅可以用来代替一维搜索，而且也可以解决Hessen矩阵不正定等困难
• 主要思想：首先选择一个步长r，使得在||x-xk||<r范围内(信赖域)；

目标函数用n维二次模型来逼近，并以此选择一个搜索方向sk，取xk+1=xk+sk。 

• 具有牛顿法的快速局部收敛性，又具有理想的总体收敛性。