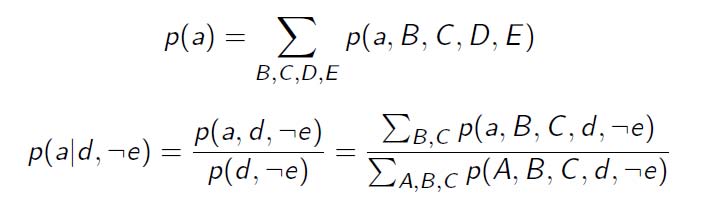Sidebar
keynote:2011-lesson04
第四课 Probabilistic Graphical Models
定义
- 对含有大量随机变量的真实问题建模
- 含有依赖关系的变量可以简化建模过程
目标
- 学习:使用训练数据估计联合分布
- 计算p(A, B, C, D, E)的概率值
- 变量数目很大怎么办?
- 推理:给定分布p(A, B, C, D, E),
- 计算某个事件发生的概率:给定E=e, 计算 A=a的概率
- 得到概率最大时对应的各个变量的状态:p(A | E=e)概率最大时A的状态
非结构化方法
- 特例:Naive Bayesian:假设变量都独立,则P(A,B,C,D,E)=P(A)P(B)P(C)P(D)P(E)
4.1 贝叶斯网络
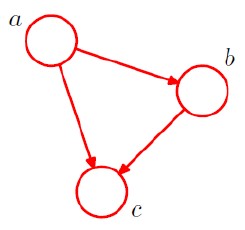
- 关于变量a,b,c的任意联合概率分布P(a,b,c)
- 概率乘法法则:p(a,b,c)=p(c|a,b)p(a,b)=p(c|a,b)p(b|a)p(a)
4.1.1 不完全连通图
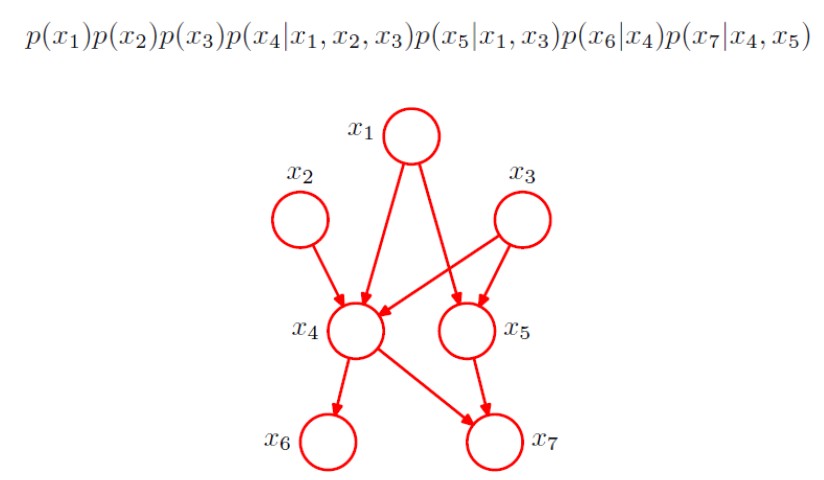
- 联合概率:p(x1,x2, … ,x7)
- e.g.
- 一般形式:
- 对于含K个节点的图,联合概率
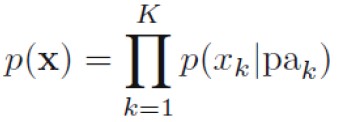 其中pak表示xk的父节点集合,x = {x1,… ,xK}
其中pak表示xk的父节点集合,x = {x1,… ,xK}
4.1.2 数学定义
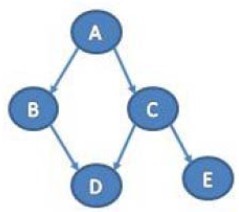
- 令G = (I,E)表示一个有向非循环图形(DAG),其中I代表图形中所有的节点的集合,而E代表有向连接线段的集合,且令X = (Xi)i ∈ I为其有向非循环图形中的某一节点i所代表之随机变数,则途中节点X的联合机率分配可以表示成:P(A), P(B|A=a), P(B|A=a), P(C|A=a), P(C|A=~a), P(D|b, c), P(D|~b, c), P(D|~b,c); P(D|~b,~c), P(E|c), P(E|~c)…
- 马尔科夫条件:每个变量都独立于其非后代的节点。
4.2 图模型的常用推导方法
- 变分法:变分贝叶斯,变分EM(参见bishop 第10章)
- 抽样法:吉布斯抽样法(参见bishop 第11章)
4.3隐马尔可夫模型
4.3.1马尔可夫性质
- 正式定义
一组随机变量序列X=\{X_n\},n=0…N,其中X_k的取值为s_k且s_k\inN,当且仅当P(X_m=s_m|X_0=s_0,…, X_{m-1}=s_{m-1})=P(X_m=s_m|X_{m-1}=s_{m-1}),则X满足马尔可夫性质。
- 非正式定义
一个过程的“将来”仅依赖“现在”而不依赖“过去”,则此过程具有马尔可夫性质。
4.3.2马尔可夫链的历史
- 马尔可夫链理论发展于1900年
- 隐马尔可夫模型发展于六十年代晚期
- 在六七十年代广泛应用于语音识别
- 1989年被引入计算机科学
4.3.3 马尔可夫链的应用
- 生物信息学
- 信号处理
- 数据分析和模式识别
4.3.4 马尔可夫链
- 一条马尔可夫链由以下三要素确定:
- 状态空间 S=\{s_1, s_2, … , s_n\}
- 初始分布 a_0
- 转移矩阵 A
4.4 最大似然估计
从一个给定的O和Q中,似然值为:\\
$L(A,B,\pi)=a_{i_1}b_{i_1o_1}a_{i_1i_2}b_{i_2o_}...a_{i_{T-1}i_T}b_{i_To_T}$\\
Log-likehood 值为\\
$l(A,B,\pi)=\sum_{i=1}^Mf_{i0}ln(a_i)+\sum_{i=1}^M\sum_{j=1}^Mf_{ij}ln(a_{ij})+\sum_{i=1}^M\sum_{o(i)}ln(b_{io})$\\
最大似然估计就是要求以下参量:\\
$a_i=\frac{f_{i0}}{1} a_ij=\frac{f_{ij}}{\sum_{j=1}^Mf_{ij}}$\\
由于直接从似然函数求最大似然估计过于困难,人们采用一些技术来计算:
- The Segmental K-means Algorith
- The Baum-Welch (E-M) Algorithm
keynote/2011-lesson04.txt · Last modified: 2023/08/19 21:02 (external edit)
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Noncommercial-Share Alike 4.0 International