High-quality Tree Structures Modelling Using Local Convolution Surface Approximation

 

The Visual Computer, 2015, 31(1): 69-82.

Xiaoqiang Zhu, Xiaogang Jin, Lihua You

 

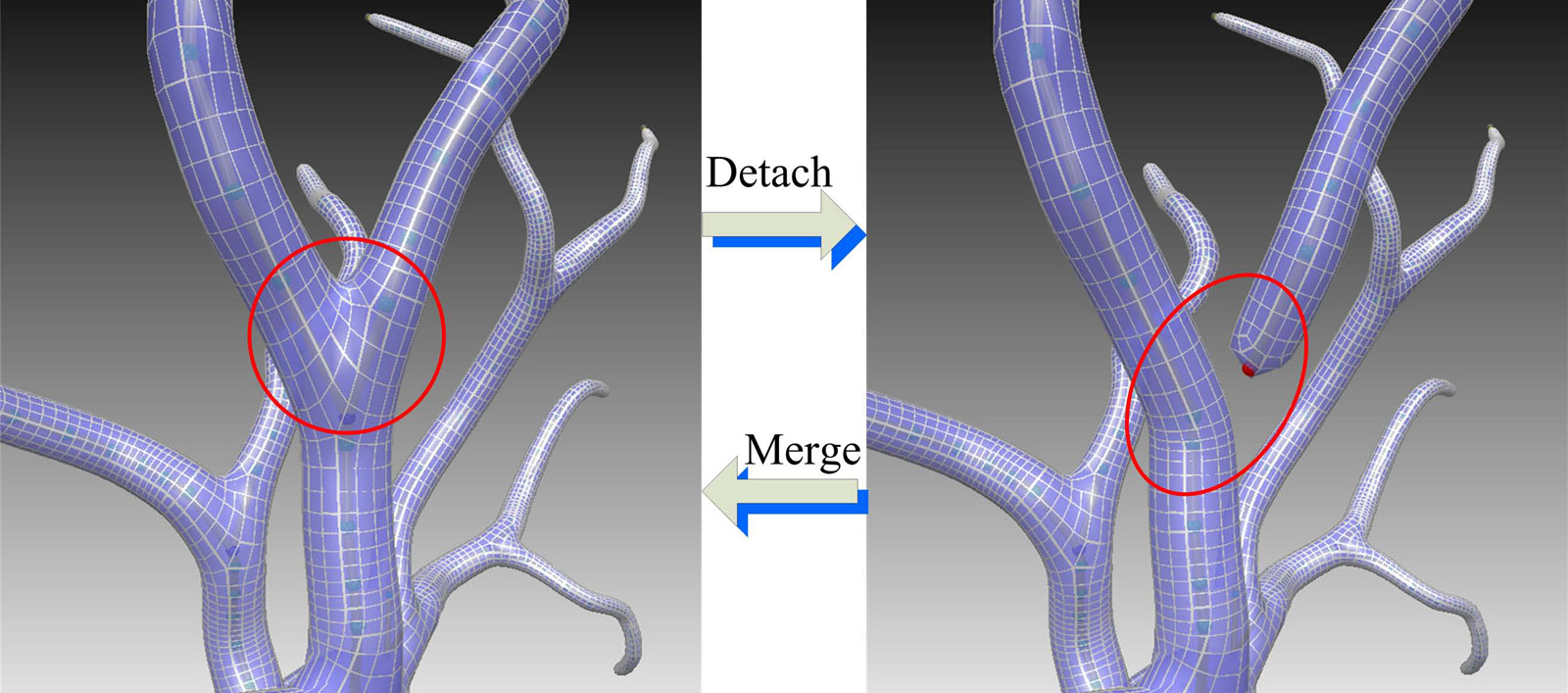
The detaching and merging procedure.

Quercus. In the first row, the images show the original tree meshes (the 1st column), the extracted line skeletons (the 2nd column), the created bounding polyhedrons (the 3rd column), the results after the second subdivision and approximation (the 4th column), and the final rendering images with texture mapping (some leaves and branchlets are additionally involved) (the 5th column). The images in the 2nd row are the newly composed trees with the subtrees generated from the one in the 1st row.

Abstract

In this paper, we propose a local convolution surface approximation approach for quickly modeling tree structures with pleasing visual effect. Using our proposed local convolution surface approximation, we present a tree modeling scheme to create the structure of a tree with a single high-quality quad-only mesh. Through combining the strengths of the convolution surfaces, subdivision surfaces and GPU, our tree modeling approach achieves high efficiency and good mesh quality. With our method, we first extract the line skeletons of given tree models by contracting the meshes with the Laplace operator. Then we approximate the original tree mesh with a convolution surface based on the extracted skeletons. Next, we tessellate the tree trunks represented by convolution surfaces into quad-only subdivision surfaces with good edge flow along the skeletal directions. We implement the most time-consuming subdivision and convolution approximation on the GPU with CUDA, and demonstrate applications of our proposed approach in branch editing and tree composition.

Download