近期,浙江大学计算机辅助设计与图形系统全国重点实验室鲍虎军和黄劲教授团队的的研究论文《GauWN: Gaussian-smoothed Winding Number and its Derivatives》(高卷数:高斯平滑卷绕数及其导数)被SIGGRAPH Asia 2024录用。该论文提出了一种新的几何处理的基础工具——高卷数(高斯平滑卷绕数),借由其可将几何形状的隐式表达与显式表达可微可导地耦合在同一个优化框架中,从而能够应用于曲线自交解除、交互编辑与偏移等应用。
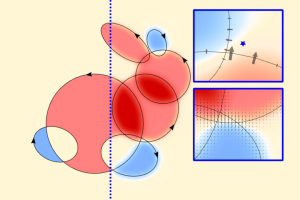
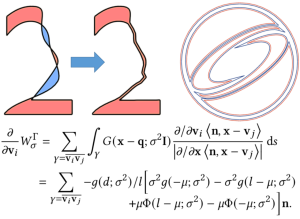
基于高卷数良好的微分性质,我们充分利用了隐式表达与显示表达各自的优点,在曲线自交解除、交互编辑、偏移等应用上得到了高效、易理解、易分析的连续优化解法。这一研究工作为多种形状表达方式的融合提供了新的可能。

