多孔模型在自然界广泛存在,如骨头、植物根茎等。这些模型经过亿万年自然选择形成,具有质量轻、性能卓越等优良特性,有广泛的产业应用前景。
首先多孔结构通常具有相对较低的密度,不仅节省材料也能减轻整体重量。模型减重在汽车、航空、航天、军工工业、医疗、材料等领域是各种设计方案能否实现的关键。其次,不同的多孔结构能够在多功能应用方面展现优良的特性。在结构功能方面,多孔模型具有高比刚度、比强度以及分散载荷的优势,能消除临界尺寸的裂纹状缺陷以及强的抗屈曲能力。在复合功能方面,多孔模性能够吸收降低噪音、屏蔽电磁辐射、且能吸收冲击能量、实现阻尼减振,或机敏控制。这些特性,使得人们可以通过多孔结构实现具有现实材料无法实现的超材料特性,在深海或深空隐身材料方面发挥具有战略价值的应用潜力。在民用方面,人们已经开始将多孔模型应用在医疗组织替换或做为细胞培养载体,或者高端运动鞋减震等方面。最近快速发展的三维打印技术使得多孔结构精确制备成为可能,为更深入地开展多孔模型研究提供了应用基础。
多孔结构设计可遵循结构——性能——功能的三段式设计原则,即通过微观结构设计实现具有一定性能的等价超材料,并在此基础上实现满足一定物理功能需求的多孔结构。然而,由于受到理论发展和计算能力的限制,传统多孔结构设计一般采用反复迭代验证的方法,根据材料性能可能覆盖的范围,调整材料有限的设计参数使之能够满足工程实际需求。此过程往往设计周期极长,在大多数情况下,设计出的结构也无法达到真正的最优化。
最理想的多孔模型设计方法是功能驱动的逆向设计方法,即从工程实际需求出发利用优化技术自动生成各类性能优越的多孔结构,以充分挖掘多孔结构的设计潜力,实现新一代功能材料和结构。
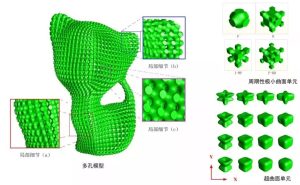
图一 双尺度多孔结构优化设计示意图
基于此研究背景,浙江大学CAD&CG国家重点实验室的高曙明教授和李明副教授的研究团队在多孔模型优化设计方面持续展开多年研究,聚焦于基础优化理论、核心计算方法、系统实现、实际应用四大方面。在理论上,推导了创新的锥拓扑优化理论,以提升优化的全局收敛性;同时,充分挖掘核心的微结构设计空间维度(含材料、方向性、分布和几何外形控制等),拓展了宏观结构功能潜力;在仿真效率上,提出了基于新型约化技术PGD的双尺度加速技巧,并实现了仿真-优化全GPU并行计算框架,大幅加速了多孔模型的仿真计算效率;在实际应用上,实现了相互连接的各向异性多孔结构优化设计,面向三维打印的自支撑多尺度优化设计,满足指定运动轨迹的形变体设计等相关研究工作。部分相关成果发表在JCAD,CMAME, IJNME, C&S,CMS等计算机辅助设计、仿真力学、计算材料等领域重要国际期刊。图一为双尺度多孔结构设计示意图。本文对部分成果给出介绍。
功能梯度多孔模型即时仿真技术。一般的三维多孔模型具有上亿自由度,对仿真计算是个极大的挑战。研究相关的高速仿真算法是实现多孔模型数字化设计的技术基础。研究团队基于均一化方法和PGD仿真技术对多孔模型实现了加速计算,尤其对功能梯度材料,可以获得在微结构改变下的即时仿真解。当用户改变了微结构的几何设计参数,或者宏观结构受力大小和方向,该方法可以即时地给出结构的物理性能。
目前尚未见相关研究工作能有效处理此问题。这里主要通过转化问题为高维度空间仿真求解问题获取,而为了(部分)克服“维度诅咒”所带来的困难,研究团队拓展了一种新型的约化解表示和求解方法Proper Generalized Decomposition (PGD),使得在解函数中各变量是相互独立的,由此大大降低了求解过程中高维积分计算的复杂度。进一步,充分利用半序多孔结构的双尺度设计特性,把微结构设计参数映射为相应的材料性能,并类似的把材料性能分布或外力映射为宏观物理性能。最终实现了微结构与宏观物理性能间的参数映射关系。此参数映射过程首先在线下求解完成,完成上述过程的求解即相当于获得了该模型所有可能参数改变情况的仿真结果。最终在线上,当用户进行设计修改时,相关物理解可直接通过函数赋值获得。
多孔结构设计空间的探索。为了设计具有卓越性能的多孔结构,微结构的设计空间本质上决定了最终可获得何种结果性能。为此,研究充分研究了多孔模型的设计空间以及相关的优化算法,依次研究了异质的各向同性圆孔或超公式、内部连通的各向异性三周期孔结构、多材料结构等,以充分获得最优结构性能。这些研究并非简单的拓展,而是在优化方法和理论上具有不同的挑战。具体来说,各向同性问题,传统上在一个宏观单元主要考虑一个设计变量,其优化相对成熟,主要挑战在于高效仿真问题。各向异性微结构优化问题,每个宏观单元涉及到多个设计变量,其难点在于如何有效地找到最优设计变量,避免局部解,获得较各向同性的更优解。对多材料优化问题,其挑战在于,总材料的可行策略总数大且难以压缩,计算难度非常高。而对几何相似的优化问题,其关键是相似度的衡量,以及在此基础上的有效结构获得问题。研究团队对上述问题进行了深入的研究,获得了突出的研究成果。
内部连通的各向异性多孔结构优化设计。以往的多孔结构仿真和设计工作由于计算能力的限制,多考虑均匀及各向同性的多孔结构。而实际上,异质的、各向异性的多孔结构拥有更多的自由度,扩大材料设计空间,有望获得更优秀的物理性能。
为此,该研究团队对传统的TPMS (Triply Periodic Minimal Surface)单元引入更多的形状控制参数,构建了具有单元各向异性的拓展的ETMPS。并在此基础上将多孔结构优化设计问题转化为对每个微观单元的几何控制参数的优化。图二对了传统的TPMS与此新型ETPMS。

A、经典的三周期微结构 TPMS

B、该团队所提出的新型三周期微结构 ETPMS
图二 传统TPMS和新提出的ETPMS对比
在优化设计过程中,需要进行多次的微观单元的均匀化计算以获得其等效的弹性张量,代价极高。为此,研究团队进一步提出了一个参数均匀化方法,借助PGD模型约化技术,在线下一次性计算获得从微观单元几何控制参数到其等效弹性张量的映射。相应的,在线上优化过程中,可以通过显式赋值,用可忽略不计的计算量获得微观结构的等效弹性张量,从而快速获得宏观结构物理性能。在此基础上,基于梯度的优化算法,可获得优化的各向异性的多孔结构。相邻单元间的几何连续性可通过几何插值算法获得。
图三描述了整体设计过程。
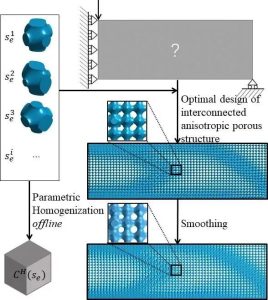
图三 相互连接的各向异性多孔结构优化设计流程图
多材料优化设计:与传统单材料拓扑优化相比,采用多种材料的设计往往能获得具有更优异的性能的目标结构。近些年来多材料3D打印机的快速发展,也使得多材料结构的制备成为可能。最近,该团队对总质量约束下的多材料拓扑优化进行了深入研究;见图四。传统多材料拓扑优化方法,一般仅考虑每个材料用量分别约束下的优化问题。而对于总材料用量约束问题,其可行策略总数大且难以压缩,计算难度非常高。该研究团队发现在确定每个材料数量的情况下,最优拓扑结构由单元的柔顺度排序唯一确定。基于此实现了两种材料的高效优化算法,并成功地转化多材料优化问题为两种材料优化问题。与传统方法相比,本方法能够以可承受的计算代价,较为有效地避开局部最优解,更好地逼近最优解。
如图五左侧,数值试验结果表明,基于传统SIMP的拓扑优化方法,在多种候选材料下,虽然获得了多材料结构,但其物理性能仍有很大改进空间。相应的,通过此新提出的方法,成功地发现仅使用两种材料即能获得更优结构。图五右侧也给出了不同候选材料下所产生的多材料拓扑优化结果。
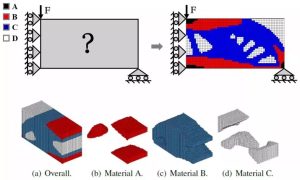
图四 材料整体重量约束
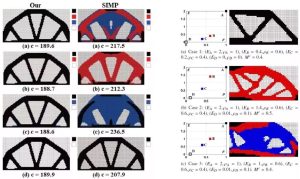
图五 约束各材料整体使用重量
纹理引导的拓扑优化:探索创新的功能结构是工程设计或几何计算的长期追求目标。不同工业领域的研究人员从各自的角度对问题进行了研究,比如着眼于内在物理性质或者外在几何外观,并提出了各种有效的途径来实现这一目标。
然而对于当前的各种研究工作,设计物理性能较优,设计美感上仍然具有很大的挑战性,这对实现具有期望局部纹理结构的设计也具有积极意义。为此,通过表达几何相似性为约束条件,该团队提出了一种新型的纹理引导的拓扑优化设计方法,该方法生成的结构在物理性能上尽可能最优,且同时能够保证与输入的示例纹理具有一定相似性。然而,直接采用上述方法,会几何断裂或突起等问题。为此,该研究团队进一步提出了创新的物理自适应的相似度度量标准,保证了最终所获得结构的物理有效性和几何光滑性。如图六对比了各种相关方法不同的效果。
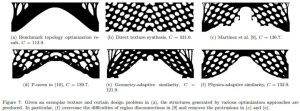
图六 各种不同方法生成优化结构对比: a、经典拓扑优化结果;b.直接纹理合成结果; c. Martines et al 结果; d. 采用P范数结果;e. 几何自适相似度结果; f.物理自适应相似度。
通过本方法,可以对一个优化设计问题,自动生成各种性能优良的设计建议,如图七所示。
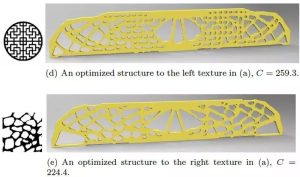

图七 纹理引导的拓扑优化结果
面向三维打印的设计优化
自支撑多尺度优化设计:对于一个复杂的轻量化三维模型,拓扑优化为其结构设计提供了理论基础,三维打印为其生产制造提供了技术保障。另一方面,由于三维打印自身的工艺性质,在打印过程中,常常会出现结构坍塌的现象,导致打印失败。为了解决这种问题,需要对打印的结构进行处理,增加一些支撑材料,在打印完成之后再将其人工去除。但这样一来,打印过程会浪费许多材料,消耗更多的打印时间。另一方面,对于打印好的模型进行人工处理支撑也是非常耗时和繁琐的过程,有些情况下甚至无法去除。
针对上述问题,该研究团队进行了基于自支撑的多尺度优化算法的研究,旨在设计出可以直接打印的自支撑结构。基于自支撑的拓扑优化算法成功解决了以下挑战:(1)直接根据自支撑的几何属性定义出的约束条件,难以与拓扑优化中的设计变量很好的结合;(2)对双尺度拓扑优化过程实现了自支撑优化设计,解决了两个尺度间自支撑条件难以统一约束的问题;(3)当计算大规模问题时,对结构进行自支撑检测会非常耗时。图八展示了自支撑拓扑优化结果。
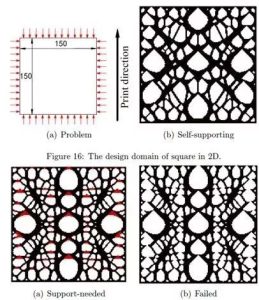

图八 通过自支撑拓扑优化方法,实现面向三维打印的自支撑结构
[1] L. Zhu, M. Li, and R. Martin. Direct simulation for CAD models undergoing parametric modifications. Special Issue of ACM Solid and Physical Modeling (SPM) 2016 in Computer-Aided Design, 2016.
[2] C. Xu, M. Li, J. Huang, S. Gao. Efficient biscale design of semiregular porous structures with desired deformation behavior. Computers & Structures, 182, 284-295, 2017.
[3] C. Xu, S. Gao, M. Li. A novel PCA-based microstructure descriptor for heterogeneous material design. Computational Materials Science, 130:39-49, 2017.
[4] X. Yang, M. Li. Discrete multi-material topology optimization under total mass constraint. Computer-Aided Design, 2018, 102: 182-192.
[5] C. Xu, M. Li, S. Gao. Performance oriented design of semiregular anisotropic porous structures. ASME IDETC/DEC, 2018.
[6] J. Hu, M. Li, S. Gao. Texture-guided generative structural designs under local control. Computer-Aided Design, 2019, 108: 1-11.
[7] D. Zhao, M. Li, Y. Liu. Self-supporting topology optimization for additive manufacturing. Under review.
[8] D. Zhao, M. Li, Y Liu, S Gao. Biscale topology optimization for high-resolution print-ready structural design. Under review.
[9] L. Zhu, M. Li, W. Xu, K. Zhou. Direct design to stress mapping for cellular structures. Under review.
[10] M. Li, Liangchao Zhu, Jingzhi Li, Kai Zhang. Optimal design of interconnected anisotropic porous structure using elliptic triply periodic minimal surface. Under review.

